(Revue CoEvolution. No 8-9. Printemps-Été 1982)
Classer un ensemble de personnes d’objets, c’est définir une limite en-deçà de laquelle telle personne ou tel objet appartient à la classe A et au-delà à la classe B. Quelle que soit la méthode adoptée, il s’agit toujours de tracer une frontière en fonction d’un critère plus ou moins arbitrairement choisi.
Cette activité intellectuelle, classer, est si ordinaire, si nécessaire au déroulement de notre pensée [1], que nous la développons sans y prendre garde et risquons de nous bercer d’illusions sur la signification du résultat obtenu. Plus précisément nous risquons de nous imaginer que les limites, que nous aurons décelées, sont des données objectives, présentes dans la nature, alors qu’elles sont le produit totalement artificiel de notre argumentation. Ainsi, l’un des premiers soins des observateurs du ciel a été de classer les étoiles qu’ils y voyaient. Ils l’ont fait « naturellement », en fonction de la caractéristique évidente qui permet de les distinguer, leur plus ou moins grand éclat. On a ainsi créé des catégories en fonction de la magnitude ; à chaque étoile était attribué un label allant de la « 1ère grandeur » à la « 21ème grandeur ». Nous risquons ainsi de diffuser l’idée que la magnitude est une propriété intrinsèque de l’étoile, alors qu’elle ne caractérise pas l’objet en lui-même, mais la vision que nous en avons ; elle correspond en fait à la résultante de deux facteurs : la brillance propre de l’étoile et son éloignement. De tout autres classements des astres sont maintenant utilisés, qui tiennent compte de facteurs bien différents, où l’apparence ne joue qu’un rôle très secondaire.
L’arbitraire du choix des critères qui nous permettent de tracer des frontières entre les objets est évident ; mais un autre arbitraire, plus sournois, doit être souligné, celui du choix d’une méthode de classification.
Deux attitudes peuvent être adoptées pour créer des catégories à l’intérieur d’un ensemble, l’une correspond à un cheminement « descendant », l’autre à un cheminement « ascendant ».
Le premier est sans doute celui que nous utilisons le plus spontanément, ainsi lorsqu’il s’agit de classer les populations humaines c’est-à-dire de définir des « races ». Nous commençons par distinguer de grands groupes en fonction du critère le plus apparent, par exemple la couleur de la peau, ce qui donne les races classiques, noire, jaune, blanche. Mais l’extrême hétérogénéité constatée à l’intérieur de chacune amène à poursuivre la classification, par exemple en fonction de la forme du crâne permettant d’opposer brachycéphales à dolichocéphales. Ce cheminement peut se poursuivre jusqu’à épuisement des critères retenu, où jusqu’à ce que chaque classe ne contienne plus qu’un objet. Il fournit des catégories qui sont à chaque stade homogènes pour tous les critères utilisés jusqu’à ce stade ; ces catégories sont donc dites monothétiques. Le résultat, souvent représenté sous forme d’un arbre, dépend non seulement des caractéristiques prises en considération, mais de l’ordre dans lequel elles interviennent. Supposons que nous ayons à classer des populations eskimo, nilotiques et pygmées ; si nous prenons comme premier critère la couleur et comme second la taille, nous obtenons
Et si nous adoptons l’ordre inverse
Pour éviter de telles discordances, il est tentant de prendre en compte toutes les caractéristiques simultanément et d’opérer une classification « ascendante ». Pour la réaliser il convient tout d’abord de synthétiser l’ensemble des ressemblances et des dissemblances entre les objets au moyen d’une distance ; soit cri la mesure du caractère r pour l’objet i ; dij, distance entre les objets i et j, est un nombre positif, défini en fonction de l’ensemble des écarts cri – crj , de façon telle que dii = 0, dij = dji et dij <= djk + dkj. Les mathématiciens ont, comme toujours, été très imaginatifs et proposé de nombreuses distances : la plus célèbre est celle d’Euclide, la plus utilisée en anthropologie celle de Mahalanobis, la préférée des généticiens des populations celle de Cavalli-Sforza ; mais bien d’autres sont disponibles.
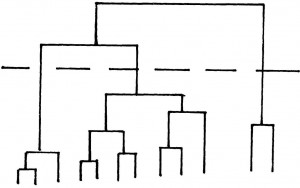
Une fois choisie une distance, plus ou moins arbitrairement en fonction de la nature des données à traiter, il s’agit de regrouper en une même classe les objets ayant entre eux une distance « faible », dans deux classes distinctes les objets ayant entre eux une distance « élevée ». Là encore de multiples méthodes ont été mises au point. Dans la pratique elles nécessitent le recours à des ordinateurs assez puissants car les calculs sont généralement laborieux. Un des cheminements possibles, lorsque objets doivent être classés, est de calculer les n(n-1)/2 distances dij, de rechercher la plus petite de ces distances, soit dkl, de remplacer les objets k et l par leur ensemble qui constitue un nouvel objet k’ se substituant à k et l, de recommencer la procédure pour le nouvel ensemble de n-1 objets, et de continuer ainsi jusqu’à obtention d’une seule classe. On obtient de cette façon un arbre tel que celui représenté ; si l’on désire un regroupement de l’ensemble en 3 classes, il suffit de couper cet arbre à la hauteur voulue mais ce nombre est évidemment arbitraire.
Finalement le pire danger de toutes ces méthodes est peut-être paradoxalement, leur efficacité. Une fois les données introduites dans la machine, il serait bien étonnant qu’une classification ne puisse être obtenue. Le risque est de lui attribuer une signification d’autant plus grande que les calculs auront été plus nombreux, et les algorithmes plus mystérieux. Nous risquons de définir des groupes, de tracer des limites qui sont un simple artefact, résultant de la manipulation que nous avons opérée sur les données, et non de la nature des choses.
Albert JACQUARD dirigea le département de génétique de l’institut National d’Études démographiques et enseigna la génétique des populations aux Universités de Paris VI, Genève et Louvain. Il est l’auteur de plusieurs ouvrages spécialisés et de « Éloge de la différence » (Seuil 1978) et « Au péril de la science ? » (Seuil 1982) etc.
[1] Voir à ce sujet le n° 2 « Penser-Classer » de la revue « Le Genre Humain » – Fayard – Janvier 1982.