(Millésime 1984)
MILLESIME – George Ifrah, vous êtes l’auteur d’une histoire universelle des chiffres (George Ifrah, « Histoire universelle des chiffres », Seghers, Paris 1981), où vous évoquez les apports de l’Orient aux systèmes de numération.
G. IFRAH – D’une manière générale, les Orientaux ont beaucoup contribué à l’essor des sciences ; aussi ont-ils été très tôt amenés à développer un outil mathématique pratique. On retrouve ainsi leur influence au niveau des nombres : toutes les grandes civilisations orientales (Egyptiens, Babyloniens, Chinois, Indiens) ont élaboré un système de numération original — Certes, ces systèmes n’ont pas tous atteint le même degré de perfection — La numération égyptienne, par exemple, comptait même parmi les plus rudimentaires. Dans ce système, de base décimale, chaque ordre d’unité était symbolisé par un signe spécifique que l’on répétait le nombre de fois requis. On lisait le nombre obtenu en additionnant mentalement les valeurs des différents symboles. Cette numération était de type additif, le plus primitif, mais aussi le plus représenté dans l’Antiquité. Les Romains par exemple, qui n’ont jamais été de brillants mathématiciens, utilisaient une numération analogue lorsqu’ils transcrivaient le nombre cent trente-deux par « CXXXII » soit « Cent plus dix, plus dix, plus dix, plus un, plus un ». Ainsi les numérations additives présentaient les deux inconvénients d’exiger d’une part autant de signes différents que le nombre à transcrire possède de rangs d’unité ; et d’autre part une répétition fastidieuse de ces signes. D’où leurs capacités très limitées.
Or c’est justement un autre peuple oriental, les Babyloniens, qui a levé le premier inconvénient. Les scribes de Mésopotamie ont dû pour cela inventer un type de numération radicalement différent du précédent : le type positionnel. Dans les numérations de position, les chiffres ont une valeur qui varie en fonction de la position qu’ils occupent dans la transcription des nombres. Ainsi le signe 4 n’a pas le même sens dans les nombres 41 et 14 où il indique le nombre des dizaines dans le premier et celui des unités dans le second (on remarque au passage que notre numération moderne relève de ce même principe élaboré sur les rives de l’Euphrate au XVIIe siècle avant notre ère…). Cette première numération de position de l’Histoire reposait sur la base sexagésimale (base soixante) dont nous avons d’ailleurs hérité pour la mesure du temps (en heures, minutes, secondes), ou des angles (en degrés, minutes, secondes). Pour les Babyloniens, la notation « 1 ; 2 ; 6 » (évidemment transcrite dans leur propre écriture) signifiait donc 1 x 602 + 2 x 60 + 6, et non pas 1 + 2 + 6 comme dans les systèmes additifs. Une étape capitale est donc franchie avec l’invention des numérations positionnelles : celles-ci permettent désormais, à l’aide d’un nombre restreint de signes, de noter simplement et rationnellement n’importe quel nombre, aussi grand soit-il. Ainsi pour écrire neuf cents en base dix, il suffit de prendre le chiffre 9 et de le décaler de deux positions ou ordres d’unité. Ceci est absolument impossible dans un système additif, où chaque chiffre symbolise une valeur définitive. D’où la nécessité d’affecter à chaque ordre d’unité un symbole distinct, ce qui encombre la mémoire sans pour autant permettre la transcription de nombres élevés : même en recourant à des conventions d’écriture, les systèmes additifs sont toujours de capacité limitée et n’ont jamais la cohésion des numérations positionnelles. On remarquera cependant que contrairement à notre système décimal actuel, le système babylonien ne disposait pas d’un nombre de chiffres égal à la base, alors que nous nous arrangeons très bien dans notre base décimale avec nos dix chiffres, il aurait été bien peu commode de manipuler soixante signes différents dans la base sexagésimale ! Pour compter entre chaque puissance de soixante, les Babyloniens recouraient à un système additif classique à base dix utilisant deux symboles : des barres horizontales figuraient les unités, et des barres verticales représentaient les dizaines. Les scribes mésopotamiens juxtaposaient ces symboles exactement comme leurs homologues égyptiens ou romains : Ainsi la graphie ![]() II = IIII se lisait (dix plus dix, plus dix, plus un, plus un) x 60 + (dix plus dix, plus un, plus un, plus un, plus un). Les « barres » sont appelées clous en raison de leur graphisme imposé par les techniques d’écriture de l’époque qui employaient des stylets à pointe sèche entaillant une plaque d’argile cuite ensuite pour conservation (écriture cunéiforme).
II = IIII se lisait (dix plus dix, plus dix, plus un, plus un) x 60 + (dix plus dix, plus un, plus un, plus un, plus un). Les « barres » sont appelées clous en raison de leur graphisme imposé par les techniques d’écriture de l’époque qui employaient des stylets à pointe sèche entaillant une plaque d’argile cuite ensuite pour conservation (écriture cunéiforme).
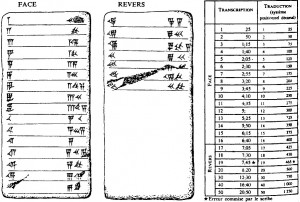
Prototypes des tables de multiplications
auxquelles les mathématiciens babyloniens
et susiens avaient recours (ci-dessus)
Si l’on estime d’après les fouilles les plus récentes que le système babylonien était parfaitement au point vers — 2000/ — 1800 avant J.-C., on sait aussi que les Babyloniens n’avaient pas encore inventé le zéro à cette époque : ils se contentaient de laisser un blanc plus ou moins grand pour symboliser un ordre d’unité vide. Aussi consciencieux que fût le scribe, la confusion devenait inévitable dès lors qu’il fallait laisser deux ou trois blancs de suite pour figurer deux ou trois zéros successifs… De même la symbolisation de l’absence d’unité en fin de nombre posait problème : par exemple on transcrivait identiquement les nombres 1 x 60, 1 x 60, 1 de la même façon que dans notre système décimal nous noterions indifféremment par « 1 » les nombres 100, 10, et 1 si nous ne disposions pas du zéro.
C’est pour résoudre ces problèmes que les scribes babyloniens ont finalement remplacé les blancs par un signe que l’on pouvait répéter clairement. Or c’est bien cette représentation concrète de l’idée abstraite d’absence, de vide, qui constitue l’invention du zéro. Le zéro fait ainsi son apparition vers 500 avant J.-C.: sa concrétisation aura exigé près de quinze siècles…
MILLESIME – Les Babyloniens ont eu une grande importance dans la mise en place de systèmes de numération — Qu’en est-il des apports des Chinois ?
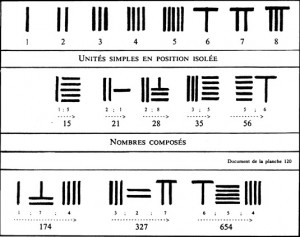
G. IFRAH – Comme les Babyloniens, les Chinois ont au début de notre ère inventé une numération de position, décimale celle-ci. Mais ils n’ont jamais découvert le zéro, qui leur a été transmis par des missionnaires bouddhistes indiens vers le 8e siècle. Comme dans le système mésopotamien, les Chinois comptaient additivement entre les puissances de la base, car ils ne disposaient pas comme nous de dix chiffres distincts. Leur unique symbole, représentant l’unité, était une barre. On passait d’un rang d’unité au suivant en changeant l’orientation des barres : « II ![]() IIII » signifiait donc (1 plus 1) x 102 + (1 + 1 + 1) x 10 + (1 + 1 + 1 + 1). Les numérations chinoises et babyloniennes étaient donc composites puisque coexistaient en quelque sorte les systèmes positionnel et additif : à l’intérieur d’un même ordre d’unité, il fallait visuellement additionner les barres chinoises ou les clous babyloniens pour obtenir le nombre de milliers, puis de centaines, etc… Tout calcul direct était dès lors impossible et il fallait systématiquement recourir au boulier. Ainsi les Chinois et les Babyloniens n’ont pas su pleinement tirer parti de leurs invention. Ce sont les Indiens, un autre peuple occidental, qui franchiront l’étape ultime en débarrassant totalement les numérations positionnelles des reliquats de système additif.
IIII » signifiait donc (1 plus 1) x 102 + (1 + 1 + 1) x 10 + (1 + 1 + 1 + 1). Les numérations chinoises et babyloniennes étaient donc composites puisque coexistaient en quelque sorte les systèmes positionnel et additif : à l’intérieur d’un même ordre d’unité, il fallait visuellement additionner les barres chinoises ou les clous babyloniens pour obtenir le nombre de milliers, puis de centaines, etc… Tout calcul direct était dès lors impossible et il fallait systématiquement recourir au boulier. Ainsi les Chinois et les Babyloniens n’ont pas su pleinement tirer parti de leurs invention. Ce sont les Indiens, un autre peuple occidental, qui franchiront l’étape ultime en débarrassant totalement les numérations positionnelles des reliquats de système additif.
Écriture des nombres composés dans le système des barres numérales chinoises
MILLESIME – Nous venons de voir que les Egyptiens et les Chinois comptaient en base décimale. De même les Grecs, les Romains, les Indiens et… nous-mêmes. Pourquoi cette base a-t-elle été si fréquemment choisie ?
G. IFRAH – Les bases de numération employées n’ont pas été à proprement parler choisies, mais devaient plutôt répondre à des impératifs essentiellement pratiques : si l’homme a presque toujours utilisé la base dix, c’est qu’il s’est principalement servi d’un instrument très commode : ses doigts. Cette explication par la morphologie humaine est la plus couramment admise : on pense même que les Mayas comptaient en base vingt parce qu’ils utilisaient également leurs orteils !
MILLESIME – Alors pourquoi une base aussi peu commode que la base soixante ?
G. IFRAH – La base sexagésimale serait née de la conjonction des bases cinq et douze utilisées par deux peuples ancêtres des Babyloniens ; 60 étant le plus petit commun multiple de 5 et de 12. La base 5 correspond naturellement à l’usage des 5 doigts de la main ; quant à a base 12, elle résulterait d’une méthode de comptage à partir des quatre fois trois phalanges des quatre premiers doigts dénombrées par le seul doigt opposable qu’est le pouce…
MILLESIME – Comment le système de numération moderne s’est-il mis en place ?
G. IFRAH – Ce système est le plus récent : il est apparu en Inde vers le 5e siècle après J.-C. C’est aussi le système le plus évolué car il permet pour la première fois de calculer rationnellement et rapidement. Il réunit pour cela trois éléments indispensables : premièrement, le caractère positionnel (nécessaire, on l’a vu, pour noter simplement les nombres élevés) ; deuxièmement, l’existence du zéro (qui lève toute ambiguïté dans la transcription d’un ou plusieurs ordres d’unité vides) ; et enfin, innovation décisive, le fait que chaque chiffre (ou nombre inférieur à la base) soit un signe spécifique qui se suffise à lui-même, au lieu d’être représenté par un nombre de barres ou de clous qu’il faut additionner mentalement pour lire le nombre. C’est donc aux Indiens que revient l’invention de nos « chiffres arabes » [1] que nous manipulons quotidiennement sans jamais songer qu’ils cachent sous leur simplicité un tel degré de perfection…
Fruit de plus de 2000 ans de tâtonnements, l’invention des Indiens est capitale : autorisant seule le calcul par retenues, elle a permis de s’affranchir enfin du boulier tout en calculant beaucoup plus rapidement : une simple multiplication qu’un petit écolier peut aujourd’hui effectuer en quelques minutes exigeait plusieurs jours de labeur aux savants chonis ou babyloniens… Bien plus, le système de numération indien a seul autorisé les applications modernes de calcul par ordinateur, par la possibilité qu’il offre de transcrire un nombre par une abstraction pure, c’est-à-dire sans faire appel à aucune perception visuelle comme l’exigeait le comptage de barres, de points, ou de clous des systèmes antérieurs. Les scientifiques s’accordent aujourd’hui pour dire que le système indien est, dans ses principes, parfait ; et que plus aucun progrès méthodologique n’est possible. Notre système de numération moderne ne pourrait être amélioré que par un changement de la base décimale jugée peu commode à certains égards, et surtout par une modification du graphisme des chiffres. Cette évolution s’est déjà fait sentir dans des domaines comme l’informatique où par exemple l’affichage numérique par cristaux liquides a quelque peu brisé les élégantes courbes des chiffres indiens… L’histoire des nombres n’est donc pas encore tout à fait terminée…
[1] L’appellation de « chiffres arabes » est erronée, et due à une longue tradition européenne (les Arabes se réfèrent d’ailleurs à notre numération en parlant de « chiffres indiens »). L’apport des Arabes dans l’histoire des nombres est assez modeste. Ils ont en fait simplement transmis l’invention des Indiens à l’Europe, où son usage s’est généralisé vers l’an 1000.