(Revue 3e Millénaire. No8 ancienne série. Mai-Juin 1983)
(Directeur de recherches au CNRS)
Élégante, la théorie de René Thom permet une approche qualitative du réel et de l’unité du monde des formes.
La théorie des catastrophes, théorie des discontinuités, des ruptures et des réorganisations, théorie de la vie, du mouvement. Cette théorie étudie aussi bien la collision de particules que les conséquences d’un mariage-catastrophe pour deux familles. Organisation d’une nouvelle famille. Mais cette théorie s’intéresse au premier chef à l’aspect qualitatif des événements. C’est pourquoi les Anglo-Saxons y sont plus sensibles que les Français trop englués dans le cartésianisme. Mais, avant d’aborder une autre fois les applications les plus fines de cette théorie, voyons avec Rui da Silveira comment cette théorie joue d’abord un rôle descriptif et topologique du réel, topologie qui utilise largement la mathématique de René Thom (Ici, rassurez-vous, point de formules ni d’équations). Rappelons enfin que René Thom a reçu la médaille Field en 1962 pour ses travaux. Cette médaille, Nobel des mathématiques, est décernée par un jury international de mathématiciens.
L’immense diversité du monde, tant inanimé que vivant, qui s’offre à notre regard est, sinon une découverte, du moins une constatation quotidienne. On pourrait presque dire que les progrès de la connaissance ne font souvent que dévoiler des différences nouvelles là où l’on ne voyait que du semblable. Parallèlement, pour exprimer cette diversité, pour dire les différences, nos moyens sont eux aussi multiples ; ils vont, par exemple, des simples mots désignant les formes et permettant de distinguer dans notre discours un ballon de « football » d’un ballon de « rugby », aux techniques sophistiquées permettant de mettre des chiffres différents sur les masses voisines des deux constituants du noyau atomique, le neutron et le proton. Devant la multiplicité des différences, l’homme a, de tous temps, essayé de dégager ce qui pourrait rassembler le dissemblable. Car, si la monotonie peut être source d’ennui, la diversité, dépourvue de toute cohérence, peut-être, à son tour, un facteur de trouble. Rechercher l’unité, cela revient, dans un langage imagé, à dégager les règles qui permettent, à partir de pièces apparemment disparates, de construire un « puzzle » dont émergera une forme particulière de cohérence. C’est encore la recherche d’une cohérence particulière, la démarche qui consiste à trouver les règles permettant d’accorder des sons entre eux, pour faire en sorte que ce qui pourrait n’être qu’une succession de bruits devienne de la musique. La recherche d’unité et de cohérence peut donc, elle aussi, revêtir bien des facettes. C’est ainsi qu’un des succès, et pas le moindre, de la loi de la gravitation de Newton, fut de dégager l’unité dans la manière dont tous les objets interagissent. L’interaction mutuelle entre une pomme et une noix obéit à la même formule mathématique que celle qui fait que la lune tourne autour de la terre et que ces deux planètes tournent à leur tour, autour du soleil.
Parmi les multiples diversités, celle qui touche aux formes a, depuis toujours, éveillé en nous l’intérêt, l’étonnement, voire la passion ; le monde qui s’offre à notre vue est un permanent spectacle où se mêlent les formes naturelles et celles que l’homme a agencées pour créer une harmonie particulière que nous appelons l’art. Mais, en regardant de plus près l’immense variété de ces formes, créations de la nature ou de l’homme, on sera étonné de découvrir qu’elles paraissent résulter d’agencements chaque fois différents d’un nombre limité de formes. De ces limitations résulte, peut-être, cette sensation que nous éprouvons à la contemplation de la nature ou d’une œuvre d’art, et que nous appelons harmonie. Remarquons en passant, que des limitations, on en trouve ailleurs que dans le domaine des formes ; ne sait-on pas en effet, que l’étonnante variété des matériaux répandus dans l’univers ne sont en fin de compte que les multiples combinaisons d’une centaine d’éléments (particules élémentaires). En fait, on pourrait dire comme P. Stevens [1] : « La nature se comporte comme un metteur en scène qui utilise les mêmes acteurs chaque soir dans des costumes différents pour des rôles différents. »
La recherche de l’unité dans le monde des formes revient donc à identifier ces acteurs et à connaître leur répertoire.
L’accomplissement, du moins en partie, d’une telle tâche, est désormais possible grâce aux travaux de René Thom [2]. Ces travaux, connus aujourd’hui d’un public déjà vaste, portent le nom de « théorie des catastrophes ». La théorie des catastrophes est, essentiellement, l’exploitation d’un certain nombre de résultats issus de la branche des mathématiques, qui constitue, en quelque sorte, le support rigoureux du qualitatif : la topologie.
La théorie de Thom connaît par ailleurs des applications remarquables dans différents domaines, dont la physique (thermodynamique, théorie de la stabilité, optique, par exemple). Je voudrais quant à moi essayer de faire partager au lecteur toute l’élégance et la simplicité qui se dégagent des applications de la théorie à un domaine qui nous est particulièrement familier et auquel nous sommes tous sensibles : le monde des formes.
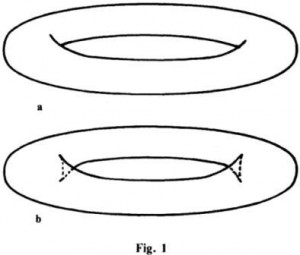
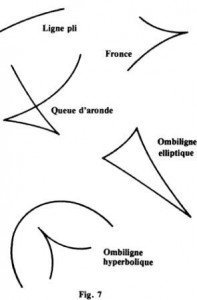
Commençons par des choses simples. Lorsqu’on observe un objet et que l’on cherche à l’identifier ou à apprécier son étendue en le parcourant du regard, on capte sur la rétine son contour apparent. Le contour apparent n’est autre que la projection dans notre rétine de la surface qui délimite l’objet. Ainsi le contour apparent d’une bille est, de toute évidence, un cercle, et celui d’un bracelet dont la section serait circulaire ressemble au dessin de la figure 1a. Si ce bracelet était translucide, sa projection apparente s’enrichirait pour ressembler alors au dessin de la figure 1b. On distingue dans ce contour une ligne extérieure fermée et continue et une ligne intérieure, fermée elle aussi, mais où l’on décèle quatre points où le contour apparent rebrousse chemin ; ce sont des points de rebroussement ou, pour utiliser le langage aujourd’hui consacré en théorie des catastrophes, des « points fronce ». Les portions continues du contour apparent sont appelées des « lignes pli ».
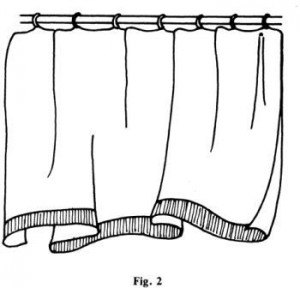
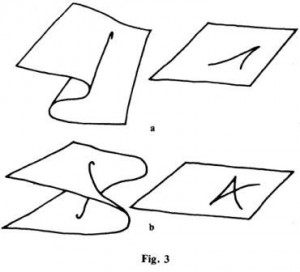
Ainsi la projection apparente du bracelet nous apparaît délimitée extérieurement par une ligne pli et, intérieurement par des lignes pli, auxquelles se greffent quatre points fronce. Ce résultat fort simple, dégagé d’une situation particulière est, en réalité, tout à fait général. Le contour apparent perçu par nos yeux des objets délimités par des surfaces lisses (sans arêtes), ne comporte que des lignes pli (c’est le cas de la bille) ou des lignes pli et des points fronce. Un exemple très commun de surface sur laquelle on peut percevoir une telle propriété est celle qui se forme sur un rideau plissé, comme l’illustre la figure 2. Si le rideau est transparent, on percevra alors dans le voisinage de l’endroit où les plis prennent naissance, le contour apparent dessiné sur le plan de la figure 3a. Cette projection apparente est encore constituée de deux lignes pli, qui se rejoignent en un point fronce. On peut maintenant essayer de construire une surface dont la projection reproduirait le dessin, plus riche, obtenu dans le cas du bracelet. Cette surface est celle de la figure 3b. Le dessin qui constitue la projection apparente de cette surface est appelé la « queue d’aronde ». La queue d’aronde est ainsi un troisième acteur que la nature met en scène et dont le répertoire contient ceux du pli et de la fronce. Pour apprécier le répertoire de la queue d’aronde, il suffit de tourner lentement le bracelet de la figure 1.
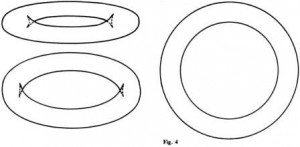
On verra alors se succéder la séquence de dessins de la figure 4 ; les quatre points fronce se rapprochent peu à peu pour se fondre deux par deux dans une simple ligne pli. Le pli, la fronce et la queue d’aronde sont les trois formes élémentaires les plus répandues. Elles constituent, en quelque sorte, les pièces de base dont la nature se sert pour révéler à notre regard le contour des objets.
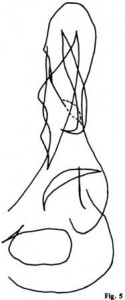
Dans la figure 5 est reproduite l’image radiologique d’un os iliaque [3]. Or l’image radiologique d’un corps n’est autre que la projection sur une plaque sensible de la surface délimitant ce corps. On ne sera donc pas étonné de reconnaître dans la figure 5 un dessin qui est un agencement particulier de lignes pli, fronces et queues d’aronde. Ainsi donc, les « puzzles » changent, mais les pièces restent les mêmes.
Mais la nature, nous dira-t-on, ne façonne pas que des contours. Elle dessine aussi. Elle dessine, par exemple, avec la lumière. Qui n’a pas observé les images aux formes capricieuses que la lumière, réfléchie ou réfractée par les objets les plus divers, dessine sur une table, un mur ou le fond d’une piscine éclairée par le soleil. Ici, plus peut-être qu’ailleurs, les formes observées paraissent résister à toute tentative d’analyse ou de réduction à des schémas simples. Pour étudier de telles images, on serait tenté de penser qu’il faudrait dresser un atlas interminable de formes. Or, il n’en est rien, car là encore ce sont toujours les mêmes acteurs qui tiennent la scène. Il n’est que trop simple de se procurer de quoi obtenir une de ces images que les opticiens appellent caustiques.
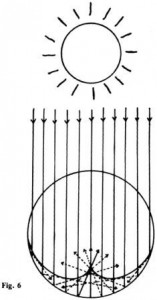
Il suffit pour cela d’exposer au soleil (ou à toute source intense de lumière) le couvercle d’une boîte ronde, métallique. Sur le fond du couvercle, on verra alors se dessiner une courbe lumineuse comme celle de la figure 6. Elle est due aux rayons lumineux que la paroi interne du couvercle focalise sur le fond. Nous sommes à même déjà de reconnaître dans cette courbe la forme d’une fronce. Si l’on dispose d’une surface réfléchissante aux formes quelque peu tourmentées, on pourra alors observer des caustiques aux formes dont la complexité paraît sans limites. En réalité, ces dessins résultent chaque fois du modelage et remodelage des cinq formes élémentaires que les trois dimensions de notre espace ont fixé une fois pour toutes. Ces cinq formes sont, d’une part, les trois formes qui nous sont déjà familières, auxquelles s’ajoutent, d’autre part, les ombiliques, elliptiques et hyperboliques, figure 7. Pour assister au répertoire de ces différents acteurs, il suffit de changer l’orientation du plan sur lequel on observe l’image. Le fond d’une piscine (dans sa partie peu profonde) est, à ce titre, une scène naturelle. Le mouvement incessant de la surface de l’eau renouvelle dans un spectacle permanent les dessins que l’on observe sur le fond.
Un article étant un texte naturellement limité, j’ai volontairement mis l’accent sur les applications de la théorie des catastrophes à un domaine restreint. De ce fait, j’ai nécessairement passé sous silence des applications non moins passionnantes de la théorie à d’autres domaines.
Le lecteur a peut-être acquis par ailleurs la conviction (les media s’en sont fait largement l’écho) du caractère très général, voire universel, de la théorie de Thom. Cette universalité se mesurerait à la diversité des domaines auxquels elle s’appliquerait ; outre la physique, la biologie, l’économie, la linguistique, le comportement animal, etc., etc.
Or les idées développées tout au long de ces quelques pages ne laissent pas entrevoir en quoi une théorie permettant de traiter des questions de morphologie permet d’aborder des sujets qui en sont aussi éloignés que le comportement animal, par exemple. Pour essayer de le comprendre (quoique de manière nécessairement superficielle), revenons un instant aux caustiques et aux surfaces délimitant les objets. Ces surfaces exhibent ce que l’on appelle des discontinuités. C’est à travers ces discontinuités, dont la projection dans notre rétine prend la forme de plis et de fronces, que l’on perçoit le contour des objets.
De même, les caustiques révèlent, elles aussi, une forme de discontinuité ! C’est en effet la discontinuité dans l’intensité de la lumière (sur le fond de la piscine, par exemple) qui dessine les différentes courbes de la figure 7.
Après tout, des discontinuités, on en trouve un peu partout : un voilier qui s’incline sous la force du vent et reprend sa position d’équilibre tant que cette inclinaison n’atteint une valeur qui le fait chavirer. Ou encore, nous savons qu’en provoquant quelqu’un par des mots, ou par des gestes, il se trouve généralement un niveau de provocation à partir duquel ce quelqu’un se met soudain en colère ; nous disons que son comportement subit un changement brusque, une discontinuité. Si des discontinuités peuvent revêtir un caractère paisible, voire harmonieux (caustiques, contours des objets), ces deux exemples montrent qu’elles peuvent aussi prendre l’allure de catastrophes !
Mais qu’y a-t-il de commun entre les deux exemples cités ? Ou, de façon plus précise, qu’est-ce qui permet d’aborder, de manière unifiée, les différentes situations où se manifestent de brusques changements ? Il se trouve, et c’est là un résultat essentiel de la théorie des catastrophes, que pour une grande partie des systèmes exhibant des discontinuités, les facteurs ou paramètres qui déterminent ces discontinuités sont liés entre eux, par des relations universelles. Qui plus est, le nombre de ces relations permettant d’aborder quantité de situations d’intérêt pratique est très limité : sept — les sept catastrophes élémentaires, pour utiliser le langage consacré.
Enfin, il est bien connu que les relations entre paramètres peuvent aussi se traduire par des courbes ou des surfaces, si l’on porte les différentes valeurs de ces paramètres sur un système d’axes. De ce fait, les sept relations universelles donnent lieu à des courbes ou surfaces qui sont, elles aussi, universelles.
Des sept catastrophes élémentaires, celles qui ne font intervenir que trois paramètres au plus sont au nombre de cinq, et peuvent être représentées par les courbes de la figure 7. Ce sont ces mêmes courbes que les trois dimensions de l’espace laissent apparaître sous forme de caustiques ! Les dessins de la figure 7 constituent les diagrammes de base sur lesquels on peut étudier une bonne partie des systèmes exhibant des discontinuités. Il faut souligner qu’il n’est pas toujours aisé d’identifier les facteurs, ou paramètres, jouant un rôle pertinent dans le déroulement d’un processus sujet à des discontinuités. D’un autre côté, s’il est facile de chiffrer, par exemple, l’intensité du vent qui détermine l’inclinaison d’un voilier, il apparaît difficile de chiffrer la provocation verbale ou gestuelle ! Dans de telles situations, faute de pouvoir manier des paramètres quantifiables, il faut se contenter d’une approche qualitative. Les diagrammes de la théorie des catastrophes fournissent à de telles approches qualitatives un support, qui semble très prometteur.
Pour le lecteur qui souhaiterait prolonger, par des textes relativement élémentaires, ce bref aperçu, voir les références bibliographiques des titres suivants :
I. Ekeland, La Théorie des catastrophes, la Recherche, n° 81, vol. VIII, 1977, p. 745.
M. V. Berry, Les Jeux de lumière dans l’eau, la Recherche, n° 92, vol. IX, 1978, p. 760.
P. T. Saunders, An introduction to catastrophe theory, Cambridge University Press, 1980.
Actes du colloque de Cerisy, Logos et Théorie des catastrophes, organisé par J. Petitot, Cerisy-la-Salle, 1982.
F. Jacob, Le Jeu des possibles, Fayard, 1981.
[1] P. S. Stevens, Les Formes dans la nature, Seuil, 1978.
[2] R. Thom, Stabilité structurelle et Morphogénèse, deuxième édition, revue, corrigée et augmentée, Inter éditions, 1977.
[3] Y. L. Kergosien, Actes du colloque « Elaboration et justification des modèles », Maloine éditeur, tome II, p. 551.