Traduction libre
« Je pense pouvoir dire sans me tromper que personne ne comprend la mécanique quantique ». Richard Feynman, lauréat du prix Nobel pour ses recherches sur l’électrodynamique quantique
INTRODUCTION
Il y a 70 ans, lorsque j’ai entendu cette citation pour la première fois (en assistant au cours de mécanique quantique de Feynman à Caltech), je me suis demandé ce qu’il voulait dire par là. Aujourd’hui, après toute une vie de recherche et d’enseignement sur la mécanique quantique, je comprends. Le formalisme mathématique de la MQ (mécanique quantique) prédit avec précision les résultats des expériences atomiques et subatomiques. Mais la façon dont nous interprétons la MQ, l’image de la réalité donnée par ces expériences, est floue et mystérieuse.
ChatGPT donne 7 interprétations de la MQ. Si vous cherchez « interprétations de la mécanique quantique » dans Wikipédia, vous trouverez une liste de 16 idées principales. Et cette liste n’inclut pas celle qui est la plus satisfaisante pour le chrétien croyant, celle qui procède des principes aristotéliciens et thomistes (je discuterai de cette interprétation plus loin). (Comme chacune de ces interprétations est cohérente avec la théorie mathématique, le formalisme de la MQ, elle ne peut être exclue empiriquement, puisque ce formalisme n’a encore été contredit par aucune expérience.
Pourquoi y a-t-il tant de façons différentes d’essayer de comprendre la MQ ? Parce que le comportement des systèmes atomiques et subatomiques dans les expériences de MQ est étrange, contre-intuitif. Je vais essayer de donner une image simple de ces comportements étranges, de ces « mystères ». Mais avant cela, permettez-moi d’exposer quelques concepts de base de la MQ. Pour une explication plus détaillée, imagée et non mathématique, le lecteur peut se référer à ce webinaire et à cet ebook.
CONCEPTS DE BASE DE LA MQ
1. La dualité onde-particule
La meilleure façon d’apprécier ce concept est de voir comment il s’est développé, c’est-à-dire d’utiliser une perspective historique (voir ici). Toutefois, pour que cet article soit bref, je me contenterai d’exposer les résultats de 27 années de recherche au début du 20e siècle.
La lumière, la chaleur, les rayons X, les micro-ondes et les ondes radio sont des rayonnements électromagnétiques. La physique classique (avant la MQ) décrivait le rayonnement électromagnétique comme des ondes. Les ondes (comme les vagues dans l’océan) s’étendent indéfiniment ; elles ne sont pas localisées, elles n’ont pas d’emplacement spécifique correspondant à un point de l’espace. Si vous faites passer un rayon de lumière à travers un trou, il peut se propager à partir du trou, c’est-à-dire que le rayon peut se courber autour d’un coin. Mais la MQ a montré que le rayonnement pouvait aussi se comporter comme une particule ; l’explication d’Einstein de l’effet photo-électrique supposait que la lumière était constituée de particules (photons) dont l’énergie était donnée par la fréquence des rayons lumineux ; plus la fréquence est élevée (plus la longueur d’onde est courte), plus l’énergie d’un photon est grande.
Selon la physique classique, les électrons, les protons, les atomes, etc. devaient être traités comme des particules, c’est-à-dire comme ayant une position spécifique en tant que point dans l’espace. En 1924, le comte de Broglie, partant de considérations sur la relativité restreinte, a postulé que les particules pouvaient se comporter comme des ondes. Sa prédiction a été confirmée en 1927 par les expériences de Davisson-Germer.
Voici quelques représentations imagées de ce comportement :
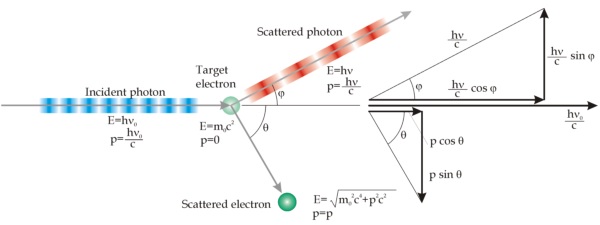
Les ondes se comportent comme des particules : l’expérience Compton :
Dans cette expérience (Arthur Compton, 1923), un photon entre en collision avec un électron au repos et rebondit, déplaçant l’électron. La conservation de la quantité de mouvement relie les longueurs d’onde du photon incident à celles du photon diffusé, ainsi que les directions du photon et de l’électron après la collision, comme le montre le diagramme ci-dessous (tiré de Wikimedia Commons ; la conservation de la quantité de mouvement signifie que la quantité de mouvement totale du photon diffusé et de l’électron déplacé est égale à la quantité de mouvement du photon incident ; ne vous préoccupez pas des mathématiques).
Compton a reçu le prix Nobel en 1927 pour ce travail.
Les particules se comportent comme des ondes : l’expérience de diffraction de la double fente
Richard Feynman a utilisé cette expérience pour initier les étudiants à la MQ. Elle illustre le comportement étrange, ondulatoire et non classique que peuvent avoir les électrons et d’autres entités atomiques et subatomiques (entités que nous considérons habituellement comme des particules). Notez tout d’abord que la lumière peut se courber autour des coins, c’est-à-dire qu’elle présente des propriétés de diffraction, comme le montre l’image ci-dessous :
Diffraction de la lumière
Les bandes vertes représentent les crêtes de l’onde électromagnétique (lumière) ; le front d’onde passe d’une onde plane (bandes vertes ascendantes et descendantes) avant de rencontrer la fente (le trou dans la ligne jaune représentant l’écran) à une onde circulaire (bandes vertes circulaires) après avoir traversé la fente. Notez que toute onde a un maximum dans la perturbation et un minimum (représenté comme négatif) et une perturbation nulle entre le maximum et le minimum.
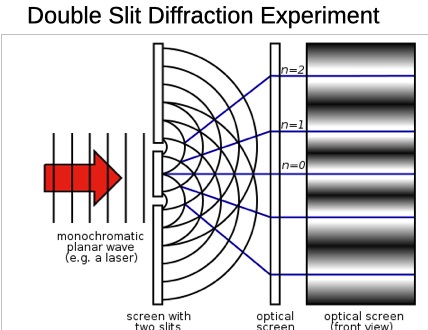
Considérons maintenant la lumière qui passe à travers deux fentes, comme le montre l’image ci-dessous.
L’onde unique est divisée en deux ondes par les fentes. Chacune de ces deux ondes a un maximum (positif) et un minimum (négatif) comme dans le diagramme ci-dessus, sauf que le maximum de l’onde passant par la fente supérieure est décalé par rapport au maximum de l’onde passant par la fente inférieure en raison de la séparation des fentes. Lorsque les maxima ou les minima des ondes coïncident, il y a une augmentation de l’intensité, observée sur un écran d’observation. Lorsque le maximum d’une onde (positive) coïncide avec le minimum de l’autre onde (négative), les deux perturbations s’annulent et l’intensité est nulle. Ainsi, le motif sur l’écran d’observation sera une série de bandes lumineuses et de bandes sombres.
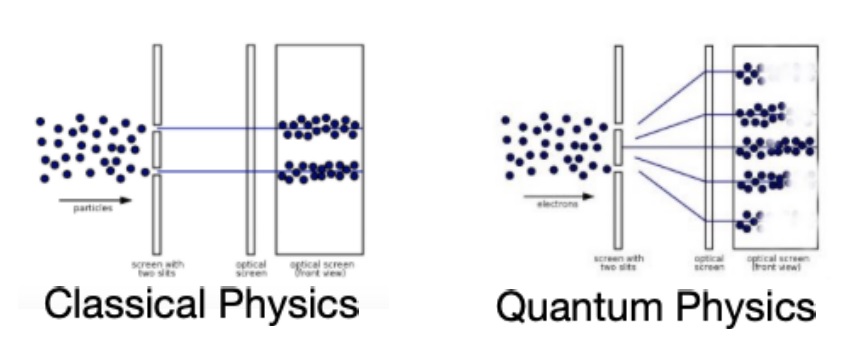
Lorsqu’une particule traverse les deux fentes, elle se comporte comme une onde jusqu’à ce qu’elle touche l’écran de détection ; elle ne s’étale pas sur l’écran, mais atterrit à un endroit précis. Après que de nombreuses particules aient traversé les deux fentes, le motif sur l’écran de détection ressemble à celui d’une onde, mais avec des points discrets où chaque particule a touché l’écran, comme le montre le diagramme ci-dessous.
Selon la physique classique, les particules passeraient à travers les fentes en ligne droite, comme le montre l’image de gauche. Selon la physique quantique, les particules se comportent comme une onde après avoir traversé les fentes, mais deviennent des particules (c’est-à-dire qu’elles sont localisées) lorsqu’elles touchent l’écran de détection.
Passons maintenant au deuxième comportement quantique étrange, l’intrication.
2. Intrication
Tout lecteur de science-fiction sait qu’il est possible de communiquer à une vitesse supérieure à celle de la lumière — regardez toutes les histoires qui l’utilisent. Cependant, la théorie de la relativité dit qu’aucune information, aucune force ne peut agir à des vitesses supérieures à celle de la lumière. Cependant, si nous observons le comportement en mécanique quantique de paires de particules (photons, électrons) produites de manière particulière, les propriétés de chacune des paires sont corrélées, et cette corrélation persiste même lorsque les paires sont séparées sur une longue distance, de sorte que l’on peut considérer cette corrélation des propriétés comme une interaction instantanée, agissant à des vitesses supérieures à celle de la lumière. Einstein a appelé ce comportement « action étrange à distance ». C’est l’une des raisons pour lesquelles il ne pensait pas que la mécanique quantique fournissait une image complète du fonctionnement de l’univers.
Pour avoir une image plus intuitive de ce qu’est l’intrication quantique, prenons un exemple qui ne relève pas de la physique. (Le faire en tant que physique nécessiterait trop de matériel de base pour ce bref article). Considérons les habitudes de vote d’un couple marié, le mari (symbolisé par H) et la femme (symbolisée par W). Chacun peut voter démocrate (symbolisé par D) ou républicain (symbolisé par R). Nous supposerons que le couple est harmonieux sur le plan politique, de sorte que l’on pourrait avoir soit (HR, WR), soit (HD, WD), c’est-à-dire que le mari et la femme votent tous les deux de la même manière. La notion d’intrication veut que même si le mari et la femme ont été séparés pendant un certain temps et sur une longue distance — dans un avenir lointain, le mari sur la Terre et la femme sur Mars ou même séparés par des années-lumière — le mari et la femme voteront de la même manière au même moment, leur vote sera toujours soit (HR, WR), soit (HD, WD).
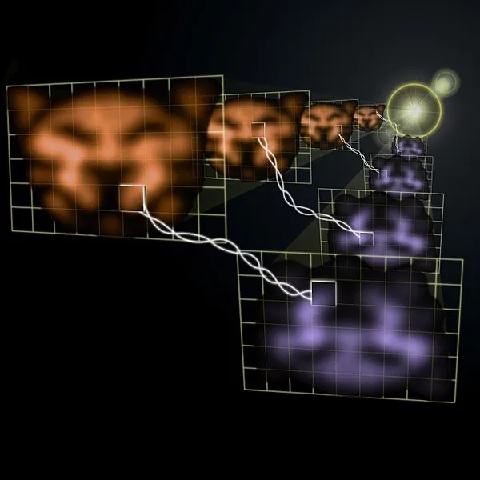
L’intrication a été vérifiée expérimentalement, même pour une paire de particules séparée par de nombreux kilomètres. L’illustration ci-dessous montre l’une de ces expériences.
Les images sont des images du visage d’un chat, transmises par deux faisceaux laser ; les photons de chaque faisceau sont intriqués. Comme les photons sont intriqués, lorsque chaque faisceau se déplace et se sépare, les fluctuations d’intensité (représentées par des petits carrés) sont les mêmes pour les parties correspondantes de l’image. (Notez que la face violette est à l’envers par rapport à la face orange ; voir ici pour un compte-rendu plus complet).
Voyons maintenant comment ces étranges comportements quantiques peuvent être interprétés d’un point de vue théologique.
LA MQ INTERPRÉTÉE : RETOUR À ARISTOTE ET AQUIN
« La seule chose qui soit pire qu’une théologie qui tente d’établir des liens entre la physique et Dieu est une théologie qui croit qu’elle n’a pas besoin de tels liens, une théologie qui croit qu’elle peut concocter le divin à partir d’un tissu métaphysique complet ». Philip Clayton, « Tracing the Lines », dans Quantum Mechanics — Scientific Perspectives on Divine Action.
Les théologiens, les philosophes et les physiciens donnent des réponses différentes à la question « La mécanique quantique parle-t-elle à la théologie ? ». Plutôt que de discuter de ces positions ici, je renvoie le lecteur à mon livre numérique, Mysteries : Quantum and Theological. Dans cet article, je me concentre sur une nouvelle façon de considérer la MQ, en utilisant des concepts de la métaphysique aristotélicienne et thomiste. Comme je ne peux pas, dans ce bref article, donner une explication détaillée de ces concepts, je donnerai des références à des ressources Internet qui donnent des explications plus complètes et je demande au lecteur de pardonner mon accent physique en parlant de philosophie.
La métaphysique aristotélicienne/thomiste pour les nuls (Moi)
Les lecteurs qui connaissent la métaphysique aristotélicienne/thomiste peuvent sauter cette section. Ceux qui ne le sont pas et qui souhaitent obtenir un compte-rendu plus complet peuvent se référer aux explications des différents termes sur YouTube ou lire l’article de Gil Sanders, An Aristotelian Approach to Quantum Mechanics (Une approche aristotélicienne de la mécanique quantique), qui donne une définition claire des termes pertinents.
Prenons l’exemple suivant d’une « chose » qui change (chose [agent de changement] -> chose changée) :
Glaçon (ajouter de la chaleur) -> eau liquide (ajouter du sel, électrolyser) -> gaz H2 et O2 (beaucoup de chaleur) -> atomes H et O
Le glaçon est une substance, il a une matière et une forme ; il a des propriétés — forme, transparence, dureté…. (« accidents ») ; il existe (« actus ») ; il peut être transformé par un agent extérieur (par exemple la chaleur) en quelque chose de différent, de l’eau liquide, il a donc la capacité (« potentia ») de se transformer. Nous pourrions procéder à d’autres transformations et changer les atomes H et O en électrons et en noyaux (protons et noyaux O16) et, plus loin encore, transformer les noyaux O16 en neutrons et en protons.
À chaque étape de cette série de changements, la « chose » est composée de ce qu’Aristote appellerait la « matière » et la « chose » a une « forme ». Il est évident que les changements impliquent certainement des changements de forme. Il est peut-être plus difficile de dire s’il y a un changement de « substance » (au sens d’Aristote). Je dirais que chacun des changements implique un changement de substance. Cependant, lorsque la question est posée à des agents d’intelligence artificielle (ChatGPT ou Bing CoPilot), on obtient des réponses différentes. Le type de matière présente est certainement différent à chaque étape. Ce qui est pertinent pour cet article, c’est qu’il existe une possibilité de changement (« potentia »), d’un état réel d’être (« actus ») à un autre.
C’est cette dernière condition qui est la plus pertinente pour expliquer l’étrangeté de MQ, et c’est cette explication que nous allons maintenant examiner.
Heisenberg invoque la potentialité quantique
Dans son livre sur la physique et la philosophie, Werner Heisenberg, pionnier de la théorie quantique, s’est tourné vers Aristote pour expliquer certains des mystères de la théorie quantique. Il attribue la nature probabiliste d’une mesure quantique au concept aristotélicien de « potentia » :
« On pourrait peut-être la traiter de tendance ou de possibilité objective, de potentia, au sens de la philosophie aristotélicienne ». Werner Heisenberg, Physique et philosophie : La révolution dans la science moderne (1958)
S’appuyant sur l’interprétation de Heisenberg, plusieurs philosophes ont développé une interprétation complète de la théorie quantique basée sur des concepts aristotéliciens/thomistes (voir Références). Je résume ces idées ci-dessous.
Mécanique quantique aristotélicienne
Selon ce physicien, les philosophes ont adopté deux approches en utilisant la métaphysique aristotélicienne/thomiste pour expliquer la MQ. La première consiste à l’intégrer dans son ensemble ; la seconde consiste à se concentrer sur les concepts de potentia (puissance, possibilité) et d’actus (réel, actuel) pour décrire la réalité. Cette dernière approche est celle de Kastner, Kauffman et Epperson (KKE), dont je parlerai plus loin.
Les KKE utilisent les termes res potentia et res extensa pour décrire la nature d’une chose (« res »). Ce qui est une res extensa est réel et peut être perçu directement par les sens ou les instruments de mesure ; ce qui est une res potentia est également réel, mais ne peut être perçu directement par les sens ou les instruments de mesure. Selon KKE, la mesure peut convertir une res potentia en res extensa, comme dans l’expérience des deux fentes :
« Considérez les deux propositions suivantes concernant une expérience à deux fentes :
X. Le photon est peut-être passé par la fente A.
Notons que nous pouvons dire de X : X est vrai ET pas X est vrai sans contradiction. Ainsi X, compris comme un énoncé de possibilité, n’obéit pas à la loi du tiers exclu. D’autre part, considérons Y :
Y. Le photon a été détecté au point P de l’écran de détection.
Y, en tant qu’énoncé sur une actualité, obéit à la loi du tiers exclu. — KKE, Prendre au sérieux la potentialité de Heisenberg.
La proposition X considère implicitement le photon incident comme une onde étendue à l’espace, c’est-à-dire que le photon peut se trouver à la fois aux deux fentes et, à moins qu’une mesure ne se produise juste après son passage à travers les fentes, il est toujours étendu à l’espace. Si le photon est mesuré juste après son passage à travers les fentes, potentia devient actus, et le photon agit comme une particule, c’est-à-dire qu’il est localisé en un point. La proposition Y considère implicitement le photon détecté en un point de l’écran comme une particule. Ainsi, la mesure (photon frappant l’écran) convertit d’une certaine manière potentia en actus, ou res potentia en res extensa. Et le même processus se produit dans le monde macroscopique, selon Aristote : un agent extérieur suffisamment puissant peut convertir la potentia d’une substance en actus, par exemple l’électrolyse peut convertir de l’eau liquide en gaz H2 et O2.
KKE expliquent l’intrication en supposant que l’acte de mesure supprime tous les états intriqués possibles, sauf un, de sorte que seul l’état mesuré subsiste. Nous pouvons examiner cette façon en utilisant l’exemple ci-dessus d’une paire mari/femme intriquée qui vote de la même manière. Considérons que l’état quantique avant la mesure est (mari, D ; femme, D) + (mari, R ; femme, R), c’est-à-dire qu’il est tout aussi probable que le couple vote pour le parti démocrate que pour le parti républicain. Alors la mesure — voter — gardera soit (mari, D ; femme, D) soit (mari, R ; femme, R). Ce sera le cas, que le mari et la femme soient séparés par un mètre ou par une année-lumière. KKE concluent que cette description d’actualités multiples est une réalité, bien qu’elle ne soit qu’une possibilité (c’est-à-dire qu’elle existe en tant que potentia quantique), et que cette intrication est indépendante des restrictions spatio-temporelles.
Si vous posez la question suivante : “Une telle interprétation aristotélicienne/thomiste ajoute-t-elle quelque chose à notre connaissance de la mécanique quantique ?” je répondrais oui, si nous considérons que cette interprétation décrit de manière générale le fonctionnement de l’univers. Ce court article n’étant qu’un amuse-bouche pour comprendre la mécanique quantique par le biais de la métaphysique aristotélicienne/thomiste, je recommande au lecteur de se reporter aux références énumérées ci-dessous pour le repas complet.
RÉFÉRENCES
Alfred Driessen, Aristotle and the Foundation of Quantum Mechanics
Gregg Jaeger, Quantum Potentiality Revisited (une explication complète de la façon dont la théorie quantique peut être placée dans un cadre métaphysique aristotélicien/thomiste)
R.E. Kastner, Stuart Kauffman, Michael Epperson, Taking Heisenberg’s Potentia Seriously (Prendre au sérieux la potentialité de Heisenberg)
Robert Koons, Knowing Nature: Aristotle, God and the Quantum; Thermal Substances: a Neo-Aristotelian Ontology of the Quantum World
Gil Sanders, An Aristotelian Approach to Quantum Mechanics (ne excellente explication intelligible de la métaphysique aristotélicienne et de son application à la compréhension de la mécanique quantique)
Guiseppe Tanzelli-Nitti, Thomism, Nature and Science
Texte original : https://www.wmbriggs.com/post/50847/
À PROPOS DE L’AUTEUR
Bob Kurland est un physicien à la retraite qui s’est converti au catholicisme en 1995. Il est diplômé de Caltech (licence avec mention, 1951), de Harvard (M.S. 1953, physique ; Ph.D. 1956, physique chimique), a mené une carrière académique à Carnegie-Mellon, SUNY/AB, MRI (Geisinger), sa meilleure œuvre scientifique étant la recherche sur l’équation Kurland-McGarvey. Il a également été bénévole dans des prisons et des hôpitaux fédéraux ; lecteur, EOMHC, et joue occasionnellement de la clarinette basse, de la clarinette alto, de la clarinette, de la basse et du psaltérion tendu ténor pour le groupe instrumental paroissial et le groupe folk local. Pour l’histoire de sa conversion, cliquez ici. Pour d’autres articles sur sa foi en tant que converti du judaïsme et scientifique, voir ici, ici et ici. Son effort actuel consiste à montrer qu’il n’y a aucune contradiction entre ce que la science dit sur le monde et la foi catholique. Des blogs intermittents et des cours d’éducation aux adultes visant à atteindre cet objectif sont disponibles sur http://rationalcatholic.blogspot.com/ et http://home.ptd.net/~rkurland).
La motivation de Bob vient de saint Augustin d’Hippone, qui a écrit dans La Trinité, 1.8 :
Mais je prie aussi le Seigneur de faire qu’en voulant instruire mes frères, je ne néglige point ma propre perfection, et qu’en répondant à leurs questions, je trouve moi-même la solution de tous mes doutes. J’entreprends donc ce traité par l’ordre et avec le secours du Seigneur notre Dieu, et je me propose bien moins d’y soutenir d’un ton magistral des vérités déjà connues, que d’approfondir ces mêmes vérités en les examinant avec une religieuse piété.