C’est précisément dans cet esprit, et afin de pouvoir dépasser la forme d’esprit déterministe inhérente à l’évolutionnisme darwinien, que j’ai estimé nécessaire d’approfondir un peu plus mes connaissances en physique théorique, avant de finir par utiliser les idées du mathématicien Luigi Fantappié et du physicien Giuseppe Arcidiacono.
Pouvez-vous exposer le contenu de ces idées ?
Je le ferai après une récapitulation panoramique de l’histoire de la physique moderne, dans la mesure où cette histoire est, en général et surtout parmi les biologistes, vraiment mal connue. Du reste, cela explique dans une large mesure pourquoi la biologie ne parvient pas encore à s’émanciper de la façon de raisonner évolutionniste, malgré le manque évident de fondements scientifiques solides qui caractérise cette dernière.
Nous pourrions revenir à notre propos en partant de Galilée qui, nous l’avons dit, était parvenu à convaincre les savants de son époque que tous les concepts généraux de la vraie science ne pouvaient être obtenus que par induction, à travers l’observation et l’expérimentation appliquées au monde sensible, considéré comme la seule réalité connaissable. Ce fut précisément en adoptant la méthode de Galilée que, tout de suite après, Isaac Newton put construire le premier grand édifice théorique de la physique moderne. Grâce aux principes de sa mécanique, bien vite on eut l’impression que tous les phénomènes naturels étaient enfin devenus compréhensibles à la raison et que même ceux qui n’étaient pas encore expliqués finiraient par se révéler conformes à ces principes. La philosophie elle-même (il suffit de penser à la Critique de la raison pure d’Emmanuel Kant) fut dominée par le cadre mécaniste.
Les grandes caractéristiques de cet édifice étaient les suivantes :
1) Les « catégories fondamentales » de chaque phénomène sont l’espace et le temps. Tout être naturel ne peut donc être représenté et défini qu’au moyen de déterminations spatiales et temporelles : de sorte que la physique traitera exclusivement des variables spatiales dans le temps, c’est-à-dire de mouvements.
2) Il est nécessaire de supposer un « quelque chose » qui accomplit ces mouvements. Ce quelque chose est la masse, caractérisée par l’inertie et par la capacité de transmettre son propre mouvement à d’autres masses à l’état de repos. Pour Kant, la masse de Newton n’est autre que le vieux concept philosophique de « substance », condensé dans une image physique précise et considéré comme vrai a priori.
3) Les différentes masses distribuées dans l’univers s’influencent tour à tour à travers des forces, dont la force de gravité n’est, peut-être, qu’un cas particulier. Ces forces, ou relations d’influence réciproque, peuvent être exprimées en termes mathématiques, par des équations, de même que les masses, les temps et les espaces.
4) Tous les mouvements se réalisent à travers une série d’états qui se succèdent de manière ininterrompue et avec une continuité absolue. Cela signifie que dans les mouvements, chaque valeur intermédiaire entre la valeur initiale et la valeur finale d’un processus physique donné est effectivement atteinte au moins une fois.
En conclusion, selon la représentation mécaniste la réalité est constituée d’un ensemble de masses ou objets matériels qui agissent les uns sur les autres selon des lois bien définies de type déterministe. D’un point de vue théorique, si l’on connaissait d’une part toutes ces lois, et d’autre part la situation précise d’un système de masses à un moment temporel donné (c’est-à-dire leurs « positions » dans l’espace et leur « vitesse » dans ce temps donné), il serait parfaitement possible de dominer par le calcul mathématique le système en question et, à la limite, tout l’univers dans son évolution globale, laquelle serait ainsi prévisible dans chacune de ses phases avec une exactitude mathématique absolue. Si nous y prêtons attention, le modèle mécaniste de la réalité propre aux XVIIIème et XIXème siècles apparaît imprégné par les traits mêmes de l’atmosphère bourgeoise au sein de laquelle il mûrit pour l’essentiel et fut ébauché : le « bon sens », la sécurité et la séparation individualiste. Les principes qui dominent en effet ce modèle, ce sont les mêmes que ceux de nos expériences quotidiennes, principes intégralement accessibles à la façon de percevoir et de raisonner de l’homme ordinaire, pour laquelle tout événement ne peut qu’obéir à un déterminisme inflexible. Quelle était l’opinion courante au XIXème siècle ? Celle-ci : « Dès lors qu’est connue la cause mécanique initiale d’un quelconque phénomène particulier, il est possible d’en prévoir les effets avec exactitude. Si nous jetons une pierre dans un étang, nous assisterons à la formation immédiate d’une série d’ondes concentriques de plus en plus étendues à partir du point de contact de la pierre avec la surface de l’eau : il ne peut y avoir le moindre doute à ce sujet. Les choses étant ainsi, il y a de quoi s’occuper. On doit analyser, expérimenter, étudier la nature jusque dans les moindres détails et inventorier soigneusement les résultats de chaque recherche. Avec le temps, nous réussirons sûrement à connaître avec précision toutes les lois auxquelles obéissent les phénomènes de la réalité et, par conséquent, à les reproduire au profit de l’humanité, réalisant pour cette dernière un mode de vie de plus en plus confortable et radieux, car privé d’inconnues inquiétantes et de superstitions fondées sur l’ignorance ».
Ainsi raisonnait-on, en s’abandonnant à un optimisme confiant (celui-là même qui transparaît, par exemple, dans les romans de Jules Verne) et à un sentiment de sécurité qu’aucune circonstance — pas même la plus risquée — ne semblait pouvoir entamer. Enfin, de même que dans le système social bourgeois chaque individu se considère comme un élément autonome, ayant, en soi, importance et valeur, indépendamment du reste de la société, de même les différents objets de la réalité sont, dans le modèle mécaniste, séparés les uns des autres et donc, à plus forte raison, de l’homme, entendu comme sujet qui les étudie. Temps, espace, masse et énergie sont vus comme autant d’individualités, chacune avec ses caractéristiques spécifiques (le temps est éternel, l’espace infini, la masse atomique, l’énergie ondulatoire), individualités qui ne sont reliées entre elles que par de simples lois de relation, et non, certes, d’équivalence ou de transformation. Les différentes disciplines scientifiques, par conséquent, fonctionnent et procèdent isolément. Par exemple, la séparation entre les propriétés de la masse et celles de l’énergie se répercute dans la séparation des sciences qui les étudient : la chimie et la physique. Cette dernière, d’ailleurs, n’est que la « somme » globale des chapitres distincts de la mécanique, de l’acoustique, de l’optique, de la thermologie, de l’électricité et du magnétisme. Quant à la biologie, elle n’est pas moins, mais encore plus séparée des autres disciplines, en raison de la singularité et de la complexité des phénomènes qu’elle étudie.
Permettez-moi une digression : selon vous, quelles furent les conséquences de la vision mécaniste dans le domaine strictement « humain » ?
Je dirais qu’il y en eut trois, toutes très importantes pour comprendre bien des traits de la mentalité moderne. Elles concernent essentiellement le problème de la « cause première », le problème posé par l’existence des phénomènes psychiques et parapsychiques, enfin le problème du libre arbitre.
Commençons par la première. Il est clair que le déterminisme du modèle mécaniste laissait irrésolu le problème d’une cause première, source originelle de la réalité et des lois qui la régissent. Toutefois, au fur et à mesure que le scientisme s’imposait, on avait tendance à répondre à la question de quatre manières différentes, à savoir : 1) soit en affirmant l’inexistence de la cause première (éternalisme) ; 2) soit en déclarant que la cause première est absolument inconnaissable (agnosticisme) ; 3) soit en plaçant aux origines le « hasard » pur et simple (casualisme [1]) ; 4) soit en admettant clairement une cause surnaturelle, mais en en limitant l’activité au seul instant de la création et en niant toute influence successive de cette cause sur le monde (déisme). Quelle que fût, en somme, l’attitude philosophique à la base du modèle mécaniste de l’univers, ce dernier cessa d’apparaître comme l’expression et la manifestation sensible, directe et constante de l’Être Suprême, c’est-à-dire comme un organisme animé de l’intérieur, toujours changeant et jamais intégralement compréhensible par l’esprit humain. Avant Newton, nul ne songeait qu’il pût y avoir des lois sans un législateur, un ordre réel compréhensible par le raisonnement mathématique sans une intelligence qui l’eût instauré. Après Newton, au contraire, on eut seulement un ensemble de « lois naturelles », entendues comme des expressions de règles purement « objectives » qui étaient enregistrées comme une donnée sensorielle quelconque. La vision du monde se réduisit à celle d’une gigantesque machine, parfaitement réglée dans l’ensemble de ses engrenages, machine dont il fallait seulement bien connaître les rouages pour en comprendre tout le fonctionnement, « charge » comprise, tandis que l’ingénieur qui avait projeté et réalisé cette machine était laissé de côté. Même avec une attitude d’inspiration religieuse comme l’attitude déiste, à quoi pouvait servir en effet un Être surnaturel dont l’œuvre s’était limitée à la construction de l’immense et éternel mécanisme de la réalité, le laissant ensuite évoluer pour son propre compte sans plus jamais l’influencer ? Un tel Être apparaissait si lointain, si englouti dans les abîmes du passé qu’il devenait comme pratiquement inexistant aux yeux de l’humanité.
Passons à la deuxième conséquence. Si la réalité se ramène à un mécanisme cyclopéen privé d’âme, d’où viennent les phénomènes psychiques ? Pourquoi les sentiments, les sensations, les émotions, les instincts, les impulsions volitives et les cas énigmatiques de manifestations paranormales ? Comment peut-on déduire des corps, uniquement définis par l’espace et le temps, un quid aussi immatériel que la pensée ? Le dualisme strict de Descartes entre monde de la matière et monde du psychisme (res extensa et res cogitans), reste donc, concrètement, irrésolu. Cependant, puisque seules la matière et l’énergie sont scientifiquement interprétables et mathématiquement définissables, avec la diffusion du scientisme on se fera à l’idée qu’il n’est possible d’avoir une connaissance exacte des deux termes de cet embarrassant dualisme qu’en les réduisant aux lois de la matière et de l’énergie. Aussi le présupposé mécaniste tendra-t-il à investir inexorablement la biologie (avec Darwin et ses épigones), mais aussi la psychologie (avec Pavlov, Freud, Watson, Skinner, Ryle, etc.).
Troisième conséquence : si la nature est une machine, alors il est évident que l’homme, qui en est partie intégrante, sera considéré comme un simple rouage de la nature. L’homme n’est donc pas artisan de la nature et de l’histoire, ce sont au contraire la nature et l’histoire qui font de lui ce qu’il est, d’époque en époque. Il s’ensuit qu’il ne peut pas y avoir de libre arbitre, tout étant soumis aux lois naturelles et — la loi de l’évolution étant admise parmi ces dernières — au « sens de l’histoire » et du progrès (historicisme, progressisme). Et de même qu’il n’existe pas de libre arbitre, de même nous devons effacer de notre vocabulaire le mot « éthique » et tout ce qu’il implique, parce que toute morale est bien sûr étrangère à la compétence d’une machine. On finit donc dans un amoralisme intégral, dont le scientifique est probablement susceptible de devenir esclave plus que quiconque. Comme l’écrit Walter Heitler : « Le monde, vie animale comprise, devient une machine insensée qui évolue selon des schémas mécanistes et quantitatifs. Cette machine se contente d’exister et rien, en elle, ne peut changer. Cette conception n’implique pas seulement une surestimation du quantitatif, mais aussi, dans le même temps, une dévaluation de tout ce qui ne s’y identifie pas, donc également une dévaluation, à la limite totale et absolue, de l’homme. Regardé sous l’angle quantitatif, l’homme est composé de très intéressantes substances chimiques dont les fonctions et réactions sont encore plus intéressantes, mais alors ce n’est plus un homme… Le fait de vouloir se limiter à l’aspect causal et quantitatif des choses a éloigné la science de l’homme » [2].
Fort bien. Pouvons-nous reprendre le fil de notre propos ?
Comme nous le disions, malgré les conséquences négatives qui s’étaient produites dans la sphère humaine, le XIXème siècle sembla s’achever dans un optimisme inséparable du triomphe total de l’interprétation mécaniste et déterministe de la réalité, donc à l’enseigne des grandes conceptions de la mécanique et de la gravitation (Newton) et de l’électromagnétisme (Maxwell) en physique, de la théorie atomique et moléculaire de Dalton, Avogadro et Cannizzaro en chimie, de la théorie nébulaire de Laplace en astronomie, des deux grandes théories évolutionniste (Darwin) et cellulaire (Schleiden et Schwann) en biologie. Mais déjà s’annonçaient, menaçants, les prodromes d’une remise en cause radicale de tant de belles constructions de la pensée humaine.
L’effet photo-électrique, le troisième principe de la thermodynamique, la radioactivité, les rayons Roentgen, les premières particules subatomiques et le résultat paradoxal de l’expérience de Michelson et de Morley (relatif à l’existence ou non du fantomatique « éther » cosmique, imaginé comme support mécanique nécessaire à la propagation des ondes électromagnétiques), voilà quels furent les premiers coups démolisseurs contre l’édifice, apparemment très solide, du XIXème siècle. Ils provoquèrent une crise profonde qui devait être surmontée peu à peu, au cours de la première moitié du XXème siècle, grâce à la révolution entraînée par la théorie de la relativité d’Albert Einstein et la théorie quantique de Max Planck.
Pour comprendre de quelle façon purent naître ces deux théories, il faut se référer à la révolution qui se vérifia dans le domaine des mathématiques au siècle dernier, lorsque Cauchy, Dini et tant d’autres soumirent les fondements de leur discipline à une critique générale. De cette critique sortit un fait d’une portée décisive : tout l’édifice de la mathématique pouvait être construit en restant dans le monde de la logique « pure ». Il n’était donc plus nécessaire de faire référence à des concepts et abstractions tirés d’expériences avec le monde sensible. En effet, alors que précédemment les postulats dont on partait étaient toujours élaborés sur la base de ces concepts et abstractions (il suffit de penser au « point », à la « droite », au « plan », etc., intuitivement rapportés, par exemple, au grain de sable, au rayon de soleil filtré par une fente et à la surface de la mer), par la suite la mathématique devint pleinement indépendante du monde qui nous entoure, se présentant exclusivement comme « science de toutes les réalités logiques possibles », c’est-à-dire privées de contradictions intrinsèques.
On a donc pu construire des édifices mathématiques très riches et très variés, en faisant totalement abstraction de leur possible correspondance effective avec les lois naturelles et en cherchant plutôt cette correspondance éventuelle dans un deuxième temps seulement. Les théories des hyperespaces, des ensembles, des groupes abstraits et des opérateurs fonctionnels, le calcul absolu de Ricci Curbastro et de Levi-Civita, la logique symbolique de Peano, les géométries de Riemann et de Lobatchevski, etc. : tout cela, ce sont des constructions de logique pure, donc non déduites, en aucune façon, d’expériences avec le monde sensible. Et sur toutes ces constructions trône le théorème de Gödel, qui affirme, en un certain sens, l’infinité des réalités mathématiques. Cela revient à dire que la mathématique constitue un ensemble infiniment riche et étendu d’où il est possible de tirer tous les schémas logiques qui se montrent les plus aptes à la résolution de n’importe quel problème cognitif, y compris du plus complexe.
Or, les « faits nouveaux » comme l’effet photo-électrique et les résultats de l’expérience de Michelson et de Morley, qui ne pouvaient être intégrés par les schémas logico-mathématiques du déterminisme mécaniste des XVIIIème et XIXème siècles, fondés sur le « bon sens » et l’expérience quotidienne courante, ne pouvaient trouver une explication cohérente qu’à condition d’être « pensés » et posés à la lumière des nouveaux schémas mathématiques. Mais ceux-ci, s’ils ne sont pas du tout évidents pour le « bon sens » commun, ne sont pas non plus adaptables à notre capacité d’imaginer les choses, inexorablement liée à un univers « euclidien » à trois dimensions seulement (longueur, largeur et hauteur). Du reste, on n’exige plus aujourd’hui d’une théorie scientifique qu’elle soit représentable à l’imagination commune, on exige seulement d’elle les trois réquisits essentiels de la cohérence logique (donnée par son appareil mathématique), de l’adéquation aux faits (avec la possibilité d’en prévoir de nouveaux) et de la progression vers l’unité du savoir (manifestée par sa capacité de faire la synthèse du plus grand nombre possible de faits réels).
En résumé, le tableau de la réalité défini par la physique de notre siècle apparaît donc beaucoup plus complexe que le tableau mécaniste et ne peut être compris par la logique limitée de nos expériences quotidiennes courantes. D’où les grandes difficultés qu’on rencontre généralement pour le faire comprendre au public. Malgré cela, un tel tableau explique les phénomènes de façon bien plus complète que le modèle de Galilée et de Newton, dont il réduit la portée de manière radicale et décisive. En effet, alors que le modèle physique du XIXème siècle se caractérisait par le « bon sens », la sécurité et la séparation, le modèle actuel présente les caractéristiques totalement opposées du paradoxe, de l’incertitude et de la fusion.
Contrairement à ce qu’on avait toujours cru, les lois qui semblent régler le monde de notre expérience quotidienne — le « mésocosme » — ne sont applicables ni aux phénomènes du microcosme (atomes et particules élémentaires), ni à ceux du macrocosme (étoiles, galaxies, quasars). Plus précisément, les lois mésocosmiques ne sont pas valables au sens absolu, mais seulement dans un sens statistique : chacune d’elles, en somme, est la résultante de composantes données et n’est valable que dans le cadre où ces composantes donnent cette résultante. Tant pis pour nous si nos capacités de perception sont limitées à des cadres bien définis et ne savent pas saisir la situation en-deçà et au-delà de ces cadres, où valent des notions apparemment ambiguës et paradoxales (mais seulement pour notre point de vue habituel) comme le « chronotope », le « nuage de probabilités », le « corpuscule-onde », l’« espace courbe », la « ligne géodésique », etc. Ici, le fameux « bon sens » bourgeois finit vraiment par prendre sa retraite !
Ceux qui désirent connaître dans ses détails la révolution produite par la physique contemporaine sur la façon de percevoir la nature, peuvent lire l’un des nombreux livres de vulgarisation publiés sur le sujet. Je me contenterai ici de rappeler que les développements de la théorie de la relativité et de la théorie quantique, qui ont eu lieu séparément, ont fini par briser peu à peu tous les éléments les plus importants de la conception mécaniste du monde : les notions de temps et d’espace absolus, la notion de particules élémentaires solides, la nature étroitement déterministe des phénomènes physiques et la prétention d’une description objective de la réalité.
Il n’a pas été facile d’arriver à ces conclusions. Elles furent formulées pour la première fois dans les années vingt par un grand solitaire, Albert Einstein, et par un groupe international de physiciens, comprenant le Danois Niels Bohr, le Français Louis de Broglie, les Autrichiens Erwin Schrödinger et Wolfgang Pauli, l’Allemand Werner Heisenberg et l’Anglais Paul Dirac, qui unirent leurs efforts par-delà les frontières pour donner naissance à l’une des périodes les plus fécondes de l’histoire de la science [3].
Des travaux de tous ces hommes il ressort, sans le moindre doute, qu’il existe une interdépendance essentielle entre tous les phénomènes de l’univers et que, par conséquent, on ne peut pas décomposer le monde en unités élémentaires ayant une existence séparée et indépendante.
Lorsqu’on étudie la matière en profondeur, en effet, on découvre qu’elle est composée, certes, de toutes petites parties, mais que celles-ci ne sont pas les « briques fondamentales » de la réalité naturelle — comme le supposaient Démocrite et Newton. Au niveau microcosmique, la poussière faite de myriades de corpuscules solides de la physique classique, se transforme en un tumultueux océan impalpable, impossible à visualiser, d’« entités attractivo-répulsives », dont l’action s’exerce par l’intermédiaire de rythmes incessants d’émission et d’absorption d’« actions élémentaires » virtuellement contenues en elles. Les actions élémentaires émises par l’une de ces entités sont immédiatement absorbées par une autre entité qui, à son tour, réagira en émettant d’autres actions élémentaires qui seront absorbées par d’autres entités analogues. La seule façon de se représenter rationnellement ce continuum agité et changeant, c’est une expression mathématique appelée « fonction d’onde de Schrödinger », dont le carré fournit la probabilité de présence de certaines actions élémentaires dans un point donné du continuum lui-même.
Ces « ondes », ou distributions de probabilités, dont se sert la physique quantique, ne représentent pas des probabilités de choses, mais plutôt des probabilités d’interconnexions entre les différentes parties d’un tout unifié. Et l’homme qui observe constitue un élément essentiel, impossible à éliminer, de ce réseau de relations compliqué.
« L’observateur constitue le dernier maillon de la chaîne des processus d’observation, écrit Capra, et les propriétés de n’importe quel objet atomique ne peuvent être comprises qu’en termes d’interaction de l’objet et de l’observateur. Cela signifie que l’idéal classique d’une description objective de la nature n’est plus valide. Le dualisme cartésien du sujet et du monde, de l’observateur et de ce qui est observé, ne peut plus être utilisé lorsqu’on traite de la matière atomique. En physique atomique, nous ne pouvons jamais parler de la nature sans, simultanément, parler de nous-mêmes » [4].
Autant la vieille science des XVIIIème et XIXème siècles avait été séparatrice, autant la nouvelle science apparaît donc portée vers une interprétation unitaire de tous les phénomènes naturels. Et, de fait, aujourd’hui chaque discipline scientifique ne peut plus procéder pour son propre compte et interfère de plus en plus avec telle ou telle autre discipline. Au point qu’il est désormais impossible de dire si le chercheur qui travaille par exemple sur l’ADN fait de la chimie, de la génétique, de la physique, de la morphologie, de la physiologie ou de l’embryologie. Ainsi, précédemment composée de plusieurs parties fondées sur des postulats distincts, et donc séparées les unes des autres, la physique fut réduite, avec James Clerk Maxwell, à deux parties : la mécanique et l’électromagnétisme. Enfin, avec tout d’abord la théorie de la relativité et la théorie quantique partiellement harmonisées par Dirac, puis avec la « théorie des modèles d’univers » de Fantappié et Arcidiacono [5], les bases logiques de tous les phénomènes naturels, phénomènes vivants compris, ont été harmonieusement coordonnées dans un ensemble unitaire. La fusion unificatrice a fini par impliquer notions et concepts autrefois réputés non seulement distincts, mais carrément antithétiques et inconciliables : espace et temps, masse et énergie, continu et discontinu, déterminisme et finalité, sujet et objet. Tous ces concepts ne cessent pas d’exister, mais se révèlent des manifestations complémentaires et différentes de la même réalité.
Nous voici donc arrivés à la « théorie des modèles d’univers ». J’aimerais que vous exposiez en détail cette conception unitaire.
C’est une théorie qu’on comprend mieux si l’on rappelle d’abord celles d’Einstein. On sait que ce dernier, en 1905, parvint à résoudre brillamment et de manière définitive le problème de l’éther en appliquant pour la première fois en physique la mathématique des hyperespaces (ou espaces à plus de trois dimensions). C’était en cela que consistait précisément la théorie de la relativité restreinte, qu’on peut formuler de la façon suivante : « Dans tous les repères inertiels : a) les lois de la nature (tant mécaniques qu’électromagnétiques) sont les mêmes ; b) la vitesse de la lumière dans le vide est la même ».
Il faut souligner que la théorie de la relativité restreinte n’a pas représenté la plus petite anomalie dans le cadre du processus normal de développement historique qui a caractérisé la science moderne depuis l’époque de Galilée. Elle a été, en somme, une étape nécessaire, qui aurait certainement été parcourue tôt ou tard, avec ou sans Einstein.
Comme l’écrit très justement Leopold Infeld : « Aujourd’hui, on ne porte pas sur les découvertes d’Einstein le même jugement qu’il y a cinquante ans. Nous savons maintenant qu’on serait arrivé à la théorie de la relativité restreinte (dont l’exactitude ne peut être mise en doute que par un fou) même sans Einstein. À sa place, Poincaré l’aurait découverte, lui qui, indépendamment d’Einstein, s’en était beaucoup approché. Il ne fait aucun doute (ce fut Einstein qui me le dit lui-même) que la théorie de la relativité restreinte aurait été formulée sans l’opuscule d’Einstein paru en 1905. Les mouvements browniens furent expliqués, indépendamment de lui, un an plus tard, et, en ce qui concerne la radiation photonique, elle aussi aurait été découverte à partir du travail fondamental de Planck et serait certainement connue aujourd’hui » [6].
Mais si tout cela est indiscutable, alors deux questions se posent tout naturellement : en quoi consiste donc, exactement, l’originalité d’Einstein ? En quel sens peut-on dire qu’il a vraiment conditionné le développement postérieur des sciences physiques ?
« Ce fut Einstein lui-même », nous révèle encore Infeld, « qui donna la réponse à ces questions, lorsque, lui ayant fait remarquer que la théorie de la relativité restreinte aurait été trouvée sans lui, il me répondit : ‘Oui, mais la théorie de la relativité générale serait encore inconnue’. Nous étions en 1938. Et c’était la vérité » [7].
Dans cette nouvelle théorie, formulée en 1914, Einstein soulignait qu’il existe une parfaite « équivalence » entre les effets inertiels et les effets gravitationnels [8], donc que si l’on voulait bâtir une théorie de la gravitation valable pour tous les systèmes — inertiels ou non — et en accord avec ce principe d’équivalence, il fallait remplacer l’espace-temps à « courbure » nulle de la relativité restreinte par un espace-temps dont la « courbure » changerait de point à point (c’est-à-dire un espace non plus euclidien, mais riemannien). Il fallait donc admettre que tous les systèmes matériels et énergétiques produisaient, par leur présence même, des « incurvations » plus ou moins accentuées dans l’espace-temps, qui se manifesteraient comme champs gravitationnels.
En d’autres termes, pour Einstein les propriétés de la matière (ou, pour reprendre le langage des physiciens, la structure géométrico-mathématique de l’espace-temps ou « chronotope ») n’étaient autre que l’effet — pur et simple — de la présence même de la matière.
Mais alors que la théorie de la relativité restreinte rencontra tout de suite un succès extraordinaire, celle de la relativité générale fut pratiquement ignorée au début, comprise par peu de gens et rejetée par la majorité des physiciens. Elle ne parvint à se répandre péniblement qu’après avoir trouvé quelques confirmations apparentes dans le domaine astronomique. Il y avait deux raisons à cela : d’une part cette théorie était très compliquée dans sa structure mathématique ; d’autre part elle était impuissante à réaliser l’unification des lois physiques fondamentales (on n’en connaissait que deux à l’époque : la mécanique-gravitation et l’électromagnétisme) dans le sillage du déterminisme de la physique classique, unification à laquelle Einstein aspirait tant.
« L’œuvre d’Einstein, écrit Gamow, se traduisit pratiquement dans la géométrisation d’une partie plus vaste de la physique : le temps devint un proche parent des trois coordonnées spatiales et les forces de gravité furent attribuées à la courbure de cet univers quadridimensionnel. Mais les forces électriques et magnétiques étaient encore en dehors du domaine de la géométrie et Einstein, qui était déjà allé très loin, concentra toutes ses énergies pour comprendre aussi le champ électromagnétique. Parmi les propriétés géométriques de l’espace à quatre dimensions, laquelle, encore inconnue, pourrait expliquer les interactions électriques et magnétiques ? Einstein lui-même et de nombreux autres ‘cointéressés’, parmi lesquels le célèbre mathématicien allemand Hermann Weyl, firent de leur mieux pour donner du champ électromagnétique une interprétation purement géométrique, mais avec une typique obstination écossaise la créature de James Clerk Maxwell, le champ électromagnétique, refusa de se laisser géométriser.
« Pendant quarante ans environ, et jusqu’à sa mort, survenue en 1955, Einstein travailla sur la ‘théorie unifiée des champs’, une théorie qui aurait dû unifier, sur une base géométrique commune, le champ électromagnétique et le champ gravitationnel. Mais on comprit au fil des ans que ce travail était sans espoir : de temps en temps, Einstein revenait sur le devant de la scène avec un nouveau groupe de formules destinées, selon lui, à résoudre enfin l’énigme de la théorie unifiée des champs, et les premières pages du New York Times et d’autres journaux du monde entier étaient alors envahies d’expressions tensorielles compliquées. Tôt ou tard cependant, les nouvelles formules se révélaient inadéquates et tout retombait dans l’obscurité jusqu’à la prochaine révélation. Les physiciens théoriciens, jeunes et vieux, ne crurent plus, peu à peu, à la possibilité de donner au champ électromagnétique une base purement géométrique (…) Quant à Einstein, il devint de plus en plus ombrageux et réticent à parler de ces questions avec d’autres physiciens (…) Son attention, peu à peu, se concentra sur les problèmes des Juifs et de la paix dans le monde, mais son esprit resta toujours lucide et aigu » [9].
Einstein vécut toujours à l’écart (« Je n’ai jamais connu quelqu’un d’aussi solitaire et d’aussi détaché », dira Infeld) et resta convaincu jusqu’au bout de la valeur de la relativité générale. Dans une lettre adressée peu avant sa mort à Infeld, qui lui avait écrit pour l’inviter à participer à la célébration du cinquantième anniversaire de la relativité restreinte qui se tint à Berlin, Einstein répondit : « Malheureusement — ou peut-être devrais-je dire grâce au ciel — je ne me sens pas assez bien pour apparaître à l’occasion de telles cérémonies officielles. Je pense qu’il serait bon que dans votre sermon soit souligné le fait que le cœur de la théorie réside dans le principe de la relativité générale, parce que la plupart des physiciens contemporains ne l’ont pas encore compris ».
Mais on a dû chercher à remédier, d’une façon ou d’une autre, aux insuffisances de la relativité générale ?
Oui. D’une part en tentant d’élargir (par exemple en introduisant une « torsion », ou une unité de mesure variable) la géométrie riemannienne de l’espace-temps, de façon à y inclure, non seulement la gravitation, mais aussi l’électromagnétisme. C’est là-dessus que reposent, en effet, les théories de Weyl, de Straneo et d’Einstein dans leurs versions successives. De l’autre, en conservant l’espace de Riemann mais en introduisant de nouvelles dimensions au-delà de la quatrième, de façon à « géométriser » aussi, par là, le champ électromagnétique. C’est la direction actuellement suivie par la plupart des physiciens, comme le prouvent les théories de Kaluza-Klein, d’Ingraham et de Podolanski. Mais il faut reconnaître qu’aucune de ces théories ne s’est avérée satisfaisante, ni sur le plan purement théorique ni sur le plan expérimental, soit parce qu’elles sont trop artificielles et simplistes, soit parce qu’elles sont incapables de donner une interprétation physique claire des nouvelles dimensions ajoutées. Par ailleurs, au fil des ans on a dû admettre le fait que les lois ou interactions fondamentales de la nature ne sont pas seulement au nombre de deux, mais de quatre (gravitationnelle, électromagnétique, nucléaire faible et nucléaire forte) ; si bien que les théories en question se sont révélées encore plus impuissantes et inadéquates quant à leurs intentions unificatrices. Aujourd’hui, une théorie du type Kaluza-Klein, par exemple, devrait recourir, pour rendre compte des quatre interactions universelles, à un espace-temps à onze dimensions !
Il semble donc que les sciences physiques ne disposent actuellement d’aucune théorie unitaire vraiment solide et prometteuse [10], à l’exception de la théorie des modèles d’univers de Fantappié et Arcidiacono que je vais maintenant vous exposer.
On ne peut pas nier que les idées unificatrices de Luigi Fantappié (1901-1956), telles qu’elles furent présentées dans les années quarante et cinquante, prêtaient le flanc à certaines critiques importantes, puisqu’elles tendaient à subdiviser les phénomènes naturels dans les deux catégories séparées des phénomènes « entropiques » (phénomènes physiques ordinaires tendant à la désorganisation uniformisatrice) et des phénomènes « syntropiques » (phénomènes biologiques tendant à l’organisation différenciatrice). Mais étant donné qu’on en était alors au tout début des recherches sur la syntropie et sur la théorie de l’information, l’erreur de Fantappié était beaucoup moins grave que ce que cherchèrent à faire croire quelques-uns de ses adversaires succombant à la jalousie et à la polémique, qui étaient alors les représentants officiels des milieux scientifiques italiens et qui visaient seulement à l’ostraciser. Mais l’œuvre ultérieure du plus fidèle des élèves de Fantappié, le physicien Giuseppe Arcidiacono, qui en a recueilli l’héritage et l’a perfectionné de façon enthousiasmante, est amplement suffisante pour montrer que les adversaires de Fantappié avaient tort et que la figure du mathématicien de Viterbe reste l’une des plus éminentes dans le panorama scientifique de ce siècle [11]. À la lumière de la théorie des modèles d’univers, la relativité générale d’Einstein, qui avait elle aussi été conçue dans le but de mener à l’unification de toutes les lois physiques, apparaît maintenant comme le principal obstacle à la réalisation de cet objectif.
Exposons donc la nouvelle théorie. En 1954 Fantappié, alors professeur à l’Institut des hautes études mathématiques de l’université de Rome, se demanda quel était le vrai problème de fond des sciences naturelles, et il en conclut qu’il consistait dans la nécessité de décider s’il faut considérer l’univers réel comme un système ordonné (donc régi par des lois uniques et valables partout sans exception), ou bien comme un système fortuit (avec des lois valables localement et transitoirement seulement). Ayant opté pour la première solution [12], Fantappié décida d’étudier systématiquement, avec les méthodes les plus modernes de l’analyse mathématique, les possibles schémas logiques ou « modèles d’univers » susceptibles d’être construits de manière purement théorique ; puis de choisir dans un deuxième temps, parmi ces schémas, celui qui se prêterait le mieux à l’intégration cohérente de tous les phénomènes observés dans la nature.
Pour cette recherche de caractère général, il partit d’une enquête épistémologique sur les prémisses de la physique. Et il comprit que, si l’univers était un système ordonné régi par des lois, il s’ensuivait que pour construire une théorie cohérente des possibles modèles d’univers, il fallait s’appuyer sur une analyse approfondie de la notion de loi. Il en résulta que cette notion n’est pas indépendante, mais au contraire étroitement associée à celle, plus simple, d’égalité. Une loi, en effet, pour être vraiment telle, ne doit pas valoir pour un phénomène particulier, mais pour toute une classe de phénomènes que nous considérons comme « égaux ». En d’autres termes, nous admettons implicitement que des phénomènes égaux sont régis par les mêmes lois, sans quoi parler de science n’aurait pas de sens. Une théorie générale des modèles d’univers doit donc se fonder principalement sur la notion d’égalité entre quantités ou phénomènes physiques.
Or, en géométrie le critère d’égalité entre deux figures géométriques est exprimé mathématiquement par un groupe d’opérations, et en fonction de la variation de ce groupe on obtient tous les types possibles de géométrie (selon le célèbre « programme d’Erlangen » de Klein). Puisque ces considérations valent aussi pour la physique, Fantappié arriva à cette très importante conclusion : à chaque groupe d’opérations on peut faire correspondre un « possible » modèle d’univers, dont les lois sont susceptibles d’être déterminées par voie purement mathématique, dès lors qu’on connaît le groupe d’opérations qui définit le critère d’égalité entre deux quantités ou phénomènes physiques.
À première vue, cette théorie peut sembler excessivement générale : non seulement parce qu’elle nous décrit les univers « possibles » sans rien nous dire sur celui dans lequel nous vivons, mais aussi parce que, le nombre de « groupes d’opérations » étant infini, il y aura aussi d’infinis modèles d’univers possibles. Toutefois, si l’on examine les choses de plus près et si on laisse de côté les pures abstractions mathématiques, on se rend compte que pour avoir des modèles susceptibles d’une interprétation physique, il est nécessaire et suffisant — comme l’a démontré Arcidiacono — de se limiter à ceux correspondant aux groupes qui décrivent les mouvements rigides de l’espace ace à n dimensions avec m = n (n —1) / 2 paramètres [13].
Nous aurons ainsi des modèles d’univers Rnm fondés sur les groupes décrivant les mouvements rigides des espaces à 5, 6, 7, …n dimensions, lesquels seront respectivement représentés par une série d’hypersphères à 4, 5, 6, … n -1 dimensions. Chacun de ces modèles est contenu dans les suivants (dont il constitue donc un cas particulier) et contient à son tour tous les précédents (les intégrant dans un système hiérarchique unitaire). Ces modèles peuvent donc être interprétés comme des perfectionnements successifs de la description physique de la réalité.
Chacun des groupes d’opérations qui se trouve à la racine de ces modèles aura une signification triple : analytique (en tant qu’il nous fournira un critère d’égalité entre quantités ou phénomènes physiques), géométrique (en tant que ses transformations refléteront des changements internes au modèle d’univers correspondant) et physique (en tant qu’il exprimera un « principe de relativité » en fonction duquel les lois physiques resteront toujours les mêmes, abstraction faite des différentes transformations possibles du groupe). L’existence du groupe, en outre, nous donnera l’assurance que le modèle d’univers correspondant sera, non seulement un système ordonné (car pour lui vaudront des lois physiques spécifiques sans ambiguïtés ni exceptions), mais aussi un système autonome (car avec les mouvements internes à la structure géométrique relative au groupe qui le caractérise, toute « fuite » hors de lui-même sera impossible).
Cela étant, il devient extrêmement intéressant d’examiner les différents modèles d’univers qui résultent de la succession hiérarchique d’hypersphères mentionnée plus haut :
1er niveau hiérarchique : univers de Newton, ou de la relativité galiléenne.
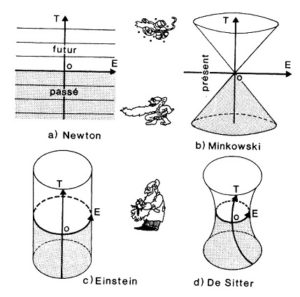
Puisque les lois de la physique classique satisfont au principe de relativité de Galilée (elles restent identiques qu’on fasse les expériences ici ou ailleurs, avant ou après, en étant arrêté ou en se déplaçant d’un mouvement rectiligne uniforme par rapport à n’importe quel autre système inertiel), il en dérive qu’elles peuvent être intégralement ramenées au groupe de Galilée, doué de 10 paramètres. A ce groupe correspond un univers où les événements physiques se déroulent dans un espace euclidien à trois dimensions, infini et illimité. En ajoutant une quatrième dimension temporelle, également infinie et illimitée, aux espaces infinis tridimensionnels qui représentent les phénomènes physiques dans leurs instants successifs, on obtient l’univers de la physique newtonienne. Cet univers a une structure « à feuilles » (comme les pages d’un livre, mais avec une dimension supplémentaire), car le temps et l’espace sont absolus et indépendants l’un de l’autre ; si bien que les évaluations de distance et de durée seront les mêmes pour tous les observateurs, indépendamment du fait que ceux-ci se déplacent ou restent immobiles (figure 1a).
2e niveau hiérarchique : univers de Minkowski, ou de la relativité restreinte.
Pour rendre compatibles les lois de la physique newtonienne avec les lois électromagnétiques, il faut considérer la vitesse de la lumière, qui dans l’univers de Newton est réputée infinie, comme finie et constante. Cela a été fait par Einstein précisément, avec sa théorie de la relativité restreinte, laquelle est exprimée mathématiquement par le groupe de Poincaré, lui aussi à 10 paramètres. L’interprétation géométrique de ce groupe avait déjà été fournie par Hermann Minkowski, qui avait démontré qu’elle ne reflétait que le groupe des mouvements internes à un espace-temps encore à quatre dimensions, mais sans la structure « à feuilles ». Dans l’univers de Minkowski, en effet, les événements se déroulent dans un espace non plus euclidien, mais pseudo-euclidien, car l’évaluation des distances et des durées finit par dépendre de l’état de mouvement particulier et relatif des observateurs par rapport aux autres systèmes physiques. Chaque point de cet univers devient donc, comme tout observateur, le centre du « cône-lumière » (figure 1b), c’est-à-dire d’un double cône — bidimensionnel sur la figure, mais à trois dimensions dans la réalité — qui divise l’univers lui-même dans les trois sections distinctes « présent », « passé » et « futur ». Et puisque la vitesse de la lumière c n’est pas infinie, un observateur quelconque ne pourra pas voir le « présent » (ni, a fortiori, le « futur »), mais seulement le « passé », c’est-à-dire uniquement le bord inférieur du cône-lumière. Il est clair qu’en faisant tendre c à l’infini, le cône-lumière a tendance à « s’écraser » dans le « présent », retombant ainsi dans l’univers de Newton. La physique classique n’est donc qu’un cas-limite de la théorie de la relativité restreinte, et seule la valeur très grande de c (300 000 km/seconde environ) peut nous permettre de comprendre pourquoi les physiciens ne sont pas parvenus, pendant si longtemps, à distinguer le groupe-limite de Galilée de celui de Poincaré.
Tandis qu’Einstein, en formulant la relativité générale et en adoptant l’espace-temps de Riemann à courbure variable (qui n’admet plus de mouvements en soi-même), abandonnait l’orientation groupale de la physique (figure 1c), Fantappié décidait d’y rester fidèle, se demandant si par hasard l’univers de la relativité n’était pas à son tour un cas-limite d’un univers plus vaste, caractérisé par un groupe encore plus généralisé. En 1954, dans une note présentée à l’« Accademia dei Lincei » [14] et publiée par celle-ci, Fantappié démontra qu’il en était effectivement ainsi. Le groupe de Poincaré s’avérait n’être précisément qu’un cas-limite d’un autre groupe, dépendant d’un paramètre r (au sens où, pour r tendant à l’infini, on obtenait de nouveau le groupe de Poincaré), que Fantappié appela groupe final, en tant qu’il ne pouvait plus représenter un cas-limite d’autres groupes à 10 paramètres. On arrive ainsi au
3e niveau hiérarchique : univers de De Sitter, ou de la relativité finale.
Après la mort de Fantappié, Arcidiacono poursuivit son œuvre et démontra que le groupe final décrit parfaitement les mouvements rigides d’une hypersphère quadridimensionnelle immergée dans une cinquième dimension, c’est-à-dire d’un espace-temps non plus « plat » comme celui de Minkowski, mais « à courbure constante positive » + 1/ r2 (r = rayon de l’hypersphère) comme celui proposé en 1917 par l’astronome hollandais Willem De Sitter (figure 1d). Ainsi, la courbure de l’univers, qui dépend étroitement, dans la relativité générale, de la simple présence de matière, dépend directement, dans la relativité finale, de la structure géométrique correspondant au groupe logico-mathématique de départ et sans aucune autre hypothèse (c’est-à-dire sans qu’il faille recourir à l’introduction « depuis l’extérieur » d’autres schémas géométriques tels le schéma riemannien).
|
Figure 1 Les principaux modèles d’univers proposés jusqu’à aujourd’hui par les sciences physiques. Les modèles sont représentés par des figures tridimensionnelles (T, temps ; E, espace ; O, observateur), même s’ils doivent être pensés comme des simplifications de structures à plus de trois dimensions. Le modèle de Newton (a) est régi par le groupe d’opérations et la relativité de Galilée. Les événements se déroulent dans un espace euclidien à trois dimensions immergé dans une quatrième dimension temporelle. Espace et temps sont absolus et indépendants, tandis que la vitesse de la lumière est infinie. Il en dérive une structure à succession uniforme, comme les pages de la tranche d’un livre (pages qui devraient cependant être imaginées non comme des plans à deux dimensions, mais comme des volumes à trois dimensions). Le modèle de Minkowski (b) est régi par le groupe d’opérations de Poincaré et la relativité restreinte d’Einstein. Les événements se déroulent dans un espace pseudo-euclidien où l’évaluation des distances et des durées dépend de l’état de mouvement particulier de l’observateur par rapport à d’autres systèmes physiques. Espace et temps sont donc relatifs et interdépendants, tandis que la vitesse de la lumière est finie. En chacun de ses points, l’univers est par conséquent divisé dans les trois régions distinctes passé, présent et avenir par un double cône-lumière (bidimensionnel sur la figure, mais à trois dimensions en réalité). Puisque la vitesse de la lumière est finie, l’observateur ne peut pas voir le présent (ni, a fortiori, l’avenir), mais seulement le passé. Si l’on fait tendre à l’infini la vitesse de la lumière, le double cône s’écrase et le modèle se transforme dans celui de Newton. Dans le modèle de la relativité générale d’Einstein (c), l’espace physique n’est plus euclidien, mais « courbe », c’est-à-dire fini et illimité comme la surface d’une sphère (qui doit cependant être pensée comme quadridimensionnelle), tandis que le temps est infini et illimité. Si nous représentons le modèle avec deux dimensions en moins, l’espace peut être comparé à un cercle qui, en se déplaçant le long de l’axe du temps, donne naissance à la surface latérale d’un cylindre. Le modèle de De Sitter (d) est régi par le groupe d’opérations et la relativité finale de Fantappié. Puisqu’ici l’espace, mais aussi le temps, sont courbes, l’univers, tout en restant fini et limité dans l’espace, et infini et illimité dans le temps (comme dans la relativité générale), n’est cependant pas toujours égal à lui-même et se manifeste comme une structure dynamique, en expansion progressive. Si l’on fait tendre à l’infini le rayon de l’univers, le modèle de De Sitter se transforme dans celui de Minkowski. |
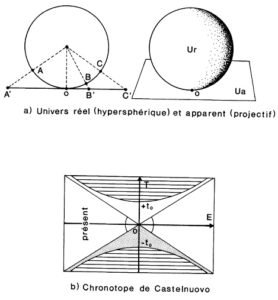
Ici se situe une importante conclusion. Comme l’a fait remarquer Arcidiacono, un univers à quatre dimensions est forcément inaccessible à notre capacité de représentation, celle-ci étant inexorablement liée à un monde tridimensionnel. Cet univers, par conséquent, nous apparaîtra à coup sûr comme différent de ce qu’il est dans sa réalité effective. C’est ainsi, par exemple, que bien que les lumières provenant des étoiles et des galaxies ne suivent pas des trajectoires rectilignes, mais des trajectoires courbes (selon les lignes géodésiques, ou grands cercles, de l’espace-temps hypersphérique), nous localiserons ces étoiles et galaxies — à cause d’un phénomène optique bien connu — dans la direction de la tangente à la trajectoire dans le point de l’hypersphère où nous effectuons l’observation. Pour savoir, par conséquent, de quelle façon nous apparaîtrait l’univers de De Sitter, nous devrions toujours nous référer à sa « projection », ou représentation sur le plan tangent en chacun de ses points (figure 2a). On obtient ainsi une nouvelle relativité, qui utilise la géométrie projective et qui a été développée de façon très fouillée par Arcidiacono.
Sur la base de cette nouvelle relativité (figure 2b), on voit immédiatement que l’univers courbe de De Sitter, qui est infini dans le temps et fini dans l’espace, doit au contraire apparaître à l’observateur comme s’il était fini dans le temps et infini dans l’espace. En d’autres termes, il se présentera comme s’il était né il y a t0 années à partir d’un point.
Je crois avoir saisi l’importance de ces conclusions. Si je ne me trompe, on retrouve ainsi, réunies en une seule théorie, les deux conceptions cosmologiques principales — et jusqu’à présent opposées — de notre siècle : celle du Big-Bang ou de l’expansion cosmique (Lemaître, Gamow, Bethe, Dicke, etc.) et celle de l’état stationnaire (Bondi, Hoyle, Gold, Narlikar).
Exactement. Il faut cependant remarquer que seule la seconde conception nous donne une « explication » de la réalité physique, la première étant essentiellement une « description » relative à notre point de vue d’êtres humains. Ce n’est pas pour rien que t0, que nous pouvons définir sans hésiter comme « âge de l’univers », se révèle être une véritable constante physique universelle, donc non susceptible d’augmenter avec l’écoulement du temps.
Contrairement à ce qu’on entend dire aujourd’hui un peu partout, la cosmologie de l’état stationnaire ne devrait donc pas être considérée comme dépassée ?
Dans le cadre de la théorie de Fantappié et Arcidiacono, cette cosmologie reste parfaitement valable et actuelle. Par ailleurs, la relativité finale s’avère trop prometteuse pour être mise de côté à la légère. Entre autres choses, pour des raisons sur lesquelles je ne peux pas m’étendre ici, elle n’admet pas seulement que la vitesse de la lumière puisse être dépassée (fournissant ainsi un bon support physico-théorique à l’existence des fameux « tachyons »), mais parvient aussi à établir un premier lien logique entre la matière et l’électricité, car elle permet d’unifier de façon simple et naturelle (bien que limitée au cas des hautes énergies, de la matière hyperdense et à l’échelle cosmique) l’électromagnétisme et l’hydrodynamique.
|
Figure 2 Le caractère hypersphérique de l’espace-temps implique que la lumière ne parcourt pas des trajectoires rectilignes, mais des arcs de cercle, ou « géodésiques ». Cela signifie que les étoiles et les galaxies ne se trouvent pas là où nous les voyons. Ce que nous observons n’est pas l’univers réel, mais un univers apparent, résultant de la « projection » de l’espace-temps hypersphérique sur l’espace euclidien qui nous est familier (a). À ce sujet, la « projection » du chronotope de De Sitter correspond au chronotope de Castel-nuovo (b), où l’espace se présente comme infini, tandis que le temps se présente comme fini. Cela signifie que l’univers apparaît en tout lieu et instant à l’observateur humain comme s’il avait commencé à partir d’un certain moment du passé (-t° : le moment de la singularité initiale ou big-bang) et comme s’il était destiné à prendre fin dans l’avenir après une quantité de temps analogue (+ t° : le moment de la singularité ou implosion finale). |
Quels autres modèles d’univers ont été définis en remontant la succession hiérarchique des hypersphères impliquée par la théorie de Fantappié et Arcidiacono ?
Si l’on reste fidèle à l’orientation groupale de la physique, on peut dire que la généralisation la plus simple de la relativité finale est fournie par la relativité résultant du groupe conforme, doué de 15 paramètres et décrivant les mouvements rigides d’un espace-temps pentadimensionnel immergé dans une sixième dimension. Nous pouvons donc parler d’un
4e niveau hiérarchique : univers conforme
Ce type de relativité n’a pas encore été formulé de manière définitive ; il en existe donc plusieurs versions, dont la plus célèbre est peut-être celle d’Ingraham, qui est d’une grande importance pour l’étude et la classification des particules élémentaires. Selon Ingraham, en effet, on peut tirer du groupe conforme les deux grands principes de complémentarité et d’indétermination auxquels obéit la physique quantique. D’autre part, l’adoption de la relativité conforme entraîne une révision profonde de la mécanique, à partir de laquelle il n’est pas du tout improbable qu’on finisse par arriver à une unification, fondée sur les groupes, de l’électromagnétisme et de la gravitation.
En 1958, Arcidiacono démontra que la relativité d’Ingraham peut être considérée comme un cas-limite d’une théorie encore plus large, susceptible de mener à une physique tout à la fois relativiste, cosmologique et quantique, et capable d’éclairer la relation existant entre ces théories [15]. Au cours des vingt dernières années, de fait, les recherches d’Arcidiacono se sont orientées dans cette direction et ont donné des résultats extrêmement significatifs. La complexité de ces recherches d’avant-garde ne me permet pas de les exposer de façon détaillée. Je me contenterai de souligner que la relativité conforme d’Arcidiacono, construite en tenant compte aussi de certains apports théoriques fondamentaux du physicien bulgare N. Kalitzine [16], est capable de mener à l’unification de l’électromagnétisme et de la gravitation. Récemment, enfin, la théorie des modèles d’univers a été utilisée par Arcidiacono dans un sens encore plus général, car il a imaginé que notre univers ne fait pas seulement partie d’univers plus vastes, mais contient à son tour des micro-univers, qui peuvent être assimilés aux particules élémentaires. Du reste, c’est précisément cette direction qu’ont prise récemment certains physiciens très connus. Piero Caldirola, par exemple, en est arrivé à concevoir l’électron comme un micro-univers de De Sitter : ce qui permet d’appliquer à ses travaux le groupe final de Fantappié et la relativité projective [17].
Votre présentation de la théorie des modèles d’univers me paraît suffisamment complète. Mais je ne comprends pas encore très bien pourquoi vous lui donnez tant d’importance dans le cadre d’une révision critique de l’évolutionnisme biologique.
Justement, j’y arrive. Le schéma des modèles d’univers inclut en effet la « théorie unitaire du monde physique et du monde biologique » formulée par Fantappié en 1944 [18]. Cette théorie introduisait l’idée selon laquelle les phénomènes naturels ne dépendent pas seulement de causes situées dans le passé, mais aussi de causes situées dans le futur [19], les deux types de causes correspondant aux deux classes de solutions, opposées mais complémentaires, qu’on obtient par les équations fondamentales de la physique quantique et relativiste : la classe des « potentiels retardés » (représentés par des ondes divergeant de la source) et celle des « potentiels anticipés » (représentés par des ondes convergeant vers la source). Alors que les solutions des potentiels retardés décrivent les phénomènes courants de nature déterministe, pour lesquels vaut la loi de l’accroissement progressif de l’entropie, avec la tendance correspondante à la désorganisation et à l’uniformité, les solutions des potentiels anticipés décrivent des phénomènes où il y a augmentation progressive d’entropie négative, ou syntropie, et donc une tendance nette à l’organisation et à la différenciation.
Fantappié faisait remarquer qu’il est parfaitement illicite de considérer a priori comme réelles les seules solutions des potentiels retardés, ce qu’on avait fait jusque-là et qu’on continue à faire. Les solutions des potentiels anticipés doivent être réputées réelles également, si bien qu’il est obligatoire d’admettre l’existence, dans la nature, des forces désorganisatrices bien connues qui gouvernent les phénomènes entropiques, mais aussi de forces actives organisées constituant un nombre non moins impressionnant de phénomènes syntropiques. Et l’exemple le plus éclatant de phénomènes syntropiques est justement constitué, pour Fantappié, par les systèmes biologiques.
Or, dans le schéma des modèles d’univers, l’existence simultanée des tendances au désordre et à l’ordre ne constitue rien de surprenant, puisqu’elle est une conséquence nécessaire des propriétés géométriques des hypersphères qui composent la succession hiérarchique des modèles eux-mêmes. En fonction de ces propriétés, en effet, une onde apparue en un point quelconque de l’hypersphère sera tout d’abord divergente, puis atteindra son expansion maximale en rapport avec le cercle maximal (ou cercle « équatorial »), et s’inversera donc, convergeant progressivement vers le point antipodique, d’où le processus s’inversera de nouveau pour donner naissance à une nouvelle onde divergente. Et il en sera de même pour tout autre point de l’espace hypersphérique.
Dans la nature, en somme, l’entropie et la syntropie sont étroitement interconnectées, et sont donc toutes deux nécessaires à une description complète de la Physis. Il n’y a donc pas (contrairement à ce qu’avait postulé Fantappié lui-même dans un premier temps) des phénomènes entropiques ou syntropiques « purs », mais seulement des phénomènes dotés d’une « composante » entropique et d’une « composante » syntropique complémentaires et interdépendantes.
Nous retrouvons donc les conclusions résumées par la phrase de Fantappié que j’ai voulu placer en exergue de notre entretien. Le fait d’avoir démontré scientifiquement que la nature est gouvernée par une complémentarité de forces désorganisatrices et de forces organisatrices, donc non seulement par ce que nous appelons simplement « matière » (ou masse-énergie), mais aussi par une véritable « forme » (on dit aujourd’hui « information »), nous renvoie directement à Aristote et, plus généralement, à la vision traditionnelle du monde. Comment ne pas songer, en effet, à la complémentarité du yin et du yang, de khouen et de khien, de prakriti et de purusha, de la substance et de l’essence, de la solutio et de la coagulatio, du mercure et du soufre des métaphysiques respectivement extrême-orientale, indienne, médiévale et hermétique ?
D’un point de vue rigoureusement scientifique, on est aujourd’hui parfaitement en droit d’interpréter le monde physique comme un système tout à la fois statique et dynamique : il est statique lorsqu’on le considère dans son ensemble, et dynamique lorsqu’on le considère dans ses éléments particuliers. Mais, de toute façon, il s’agit dans ce cas d’un dynamisme actif, cybernétique, non-évolutionniste, un dynamisme où, du fait de l’existence complémentaire de l’entropie et de la syntropie, l’« avant » conditionne l’« après » et réciproquement, dans un ensemble harmonieux d’interactions qui ne peut absolument pas être réduit à un simple jeu mécaniste et fortuit comme le prétendait Darwin.
C’est surtout en pensant constamment à la révolution conceptuelle produite par la physique que j’ai pu mener sans crainte et sans hésitation ma critique de l’évolutionnisme biologique. Et c’est précisément la vision « cosmique » — au sens antique du terme — telle qu’elle se dégage de cette révolution, que j’ai cru devoir opposer à l’évolutionnisme, ridiculement attaché à l’illusion que tout peut être modelé par l’action aveugle du hasard et de la nécessité. Cette vision ne nie pas du tout qu’il y ait des changements dans la nature ; mais elle les considère comme causés par les lois qui président à toute l’architecture spatio-temporelle du « Systema Naturae ». Ainsi sont définitivement mis de côté l’évolutionnisme, bien sûr, mais aussi un fixisme trop rigide et naïf, désormais insoutenable et anachronique.
Il est donc faux d’affirmer, comme beaucoup l’ont fait, qu’avec Dopo Darwin j’ai simplement critiqué sans proposer d’alternative. Mon alternative n’est autre que la vision traditionnelle de la réalité, mais formulée dans la terminologie scientifique moderne.
(Extrait de La Révolution organiciste – entretien sur les nouveaux courants scientifiques)
_______________________________________________
1 « Casualisme n’est pas usuel en français », écrit André Lalande dans son Vocabulaire technique et critique de la philosophie, 13ème éd., PUF, 1980, p. 1155. Nous l’avons néanmoins parfois employé, plus ou moins dans le sens d’« indéterminisme », les philosophes ayant refusé le terme tychisme (du grec tukhé = hasard), techniquement plus précis, proposé par C. S. Peirce en 1892. En français, « casuel » est synonyme d’« accidentel, contingent, fortuit ». (N.D.T.)
2Walter Heitler, Causalità e teleologia nelle scienze della natura (trad. it. de Der Mensch und die naturwissenschaftliche Erkenntnis, Braunschweig, 1962), Boringhieri, Torino, 1967, pp. 55-56.
3 Cf. George Gamow, Trent’anni che sconvolsero la fisica (trad. it. de Thirty Years that Shook Physics, Anchor Books, Doubleday and Co., New York, 1966), Zanichelli, Bologna, 1966.
4 Fritjof Capra, Le Tao de la physique, op. cit., p. 71.
5 Voir à ce sujet : Luigi Fantappié, Nuove vie per la scienza, Sansoni, Firenze, 1961 ; et de Giuseppe Arcidiacono, les ouvrages suivants : Universo e relatività, Massimo, Milano, 1967 ; Relatività e cosmologia, Veschi, Roma, 1979 ; Relatività ed esistenza, Studium Christi, Roma, 1973 ; Oltre la quarta dimensione, Il Fuoco, Roma, 1980. Différents textes s’inspirant de la conception unitaire de Fantappié et d’Arcidiacono ont paru dans la revue Responsabilità del Sapere, publiée par le Centre International de Comparaison et de Synthèse (Rome).
6 Leopold Infeld, Il mio amico Einstein, in Nuova Scienza, XX, 3, 1979, p. 58.
7 Leopold Infeld, Art. cité, ibidem.
8 Un astronaute enfermé dans un vaisseau spatial sans hublots et se sentant poussé vers une des parois, ne pourrait établir si le phénomène est dû à l’attraction de quelque corps céleste ou à la poussée inertielle du vaisseau spatial qui s’est tout à coup déplacé dans la direction opposée à la paroi elle-même.
9 George Gamow, Biografia della fisica (trad. it. de Biography of Physics, Harper, New York, 1961), EST Mondadori, Milano, 1963, pp. 204-205.
10 Le seul résultat important obtenu au cours de ces dernières années n’est autre que la « théorie électrofaible » de Higgs, Weinberg, Salam et Ward, formulée en 1967. Cette théorie unifie l’électromagnétisme et la force nucléaire faible. Supposant l’existence de deux nouvelles particules appelées W et Z, la théorie en question a trouvé une confirmation spectaculaire au CERN de Genève, en 1983, grâce à Carlo Rubbia.
11 Pour une biographie et une présentation détaillée des principaux travaux de Luigi Fantappié, cf. Giuseppe Arcidiacono, Fantappié e gli Universi, Il Fuoco, Roma, 1986.
12 Ce choix se fonde sur l’hypothèse, qui s’est toujours révélée plausible jusqu’à présent, selon laquelle les lois physiques valables pour notre Terre — ou, disons, pour notre système stellaire — peuvent être appliquées à tout l’univers. Cette hypothèse est pleinement justifiée parce qu’elle est la seule raisonnable et donc aussi la seule possible sur le plan de la recherche scientifique, si bien que le chercheur peut s’en servir en ayant la conscience tranquille. Mais cela n’enlève rien au fait qu’elle reste, naturellement, une simple hypothèse.
13 Nous devons ici renvoyer le lecteur désireux de comprendre de façon plus précise la signification de ces paramètres au livre déjà cité d’Arcidiacono, Oltre la quarta dimensions.
14 Luigi Fantappié, Su una nuova teoria di relatività finale, in Rend. Atti Accad. Naz. Lincei, série 8, XVII, 5, 1954.
15 Giuseppe Arcidiacono, La relatività di Fantappié, in Collectanea Mathematica, 1958.
16 Kalitzine s’était proposé de généraliser la relativité restreinte à un espace euclidien de n dimensions, en soutenant que d’un point de vue purement logique, rien n’oblige à accepter l’idée que notre univers ne compte vraiment que 4 dimensions, et non pas 5, 6, n ou carrément d’infinies dimensions. Il est alors nécessaire d’aborder le problème de la signification physique des nouvelles dimensions, et puisque nous ne voyons pas les corps qui nous entourent apparaître ou disparaître pour se déplacer ensuite dans des dimensions « autres », nous devons accepter l’idée que celles-ci sont toutes des dimensions temporelles. La « relativité multitemporelle » de Kalitzine, théorie restée inachevée à la mort de son fondateur, est en effet fondée sur un espace euclidien à n dimensions, dont 3 dimensions spatiales et n-3 dimensions temporelles. En 1978, G. Arcidiacono (cf. Atti del III Congresso di Relatività Generale e Gravitazione, in Atti Accademia delle Scienze di Torino) a donné une interprétation physique simple de la théorie de Kalitzine, obtenant, dans le cas d’un espace à n-5 dimensions, une « relativité conforme » à deux temps qui unifie l’électromagnétisme et la gravitation à l’intérieur du schéma de la théorie groupale des modèles d’univers.
17 Piero Caldirola, The Chronon in the Quantum Theory of Electron and the Existence of Heavy Leptons, in Nuovo Cimento, XXV, 284, 1979.
18 Luigi Fantappié, Principi di una teoria unitaria del mondo fisico e biologico, Humanitas Nova, Roma, 1944.
19 Plus tard, lors d’une conférence intitulée « Un nouveau concept d’Existence » et prononcée le 19 mai 1947 dans la grande salle de la faculté des lettres et de philosophie de l’université de Rome, Fantappié s’appuiera sur la théorie de la relativité pour étendre le concept d’existence, précédemment limité au présent, au passé et au futur (existence totale).
20Giuseppe Sermonti et Roberto Fondi, Dopo Darwin. Critica all’evoluzionismo, Rusconi, Milano, 1982 (4ème édition).
21 Né en 1925, Giuseppe Sermonti a étudié la génétique des micro-organismes à l’Institut de la Santé de Rome, de 1950 1965. Il a publié Genetics of Antibiotic Producing Microorganismus (1969), II crepuscolo dello scientismo (1971), Genetica Generale (1971 et 1974), La mela di Adamo e la mela di Newton (1974), Le forme della vita (1981). Depuis 1974, Giuseppe Sermonti est professeur de génétique à l’université de Pérouse, où il dirige l’Institut d’Histologie et d’Embryologie. Il s’est rendu à Moscou en 1978 en tant que vice-président du XIVème Congrès international de génétique. Le professeur Sermonti dirige, depuis la fin de l’année 1979, la Rivista di Biologia (N.D.T.).